The Scissors Are Back (Count 'em All 23!)
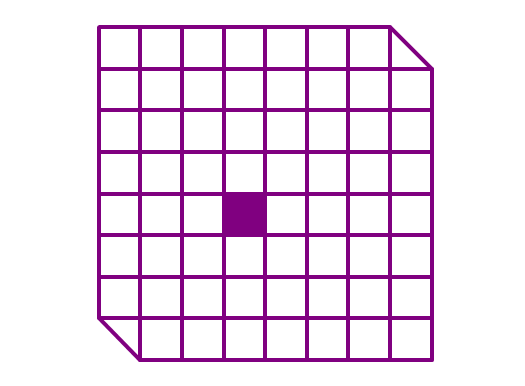
The figure above shows an grid with a hole in it, and also with 2 opposite corners cut off forming triangles to spice things up. :D
Count the total number of quadrilaterals in the grid above.
Clarifications :
- A quadrilateral is a polygon that has 4 sides.
- As usual, the quadrilaterals cannot contain the hole, because I don't like holes.
This is one part of Quadrilatorics .
The answer is 837.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's first pretend that the grid is 'perfect': it has no holes, and no cut corners. Let's also patch the cut corners with imaginary golden squares.
For convenience sake, I'll label the two golden squares A and B , and the hole C .
From this note , we know that the number of quadrilaterals in an 8 × 8 perfect grid is ( 2 9 ) × ( 2 9 ) = 4 8 × 8 × 9 × 9 = 1 2 9 6
Now we need to remove all 'invalid' quadrilaterals, invalid quadrilaterals consists of those which contain the hole, and those that turn into a pentagon or triangle when the golden corner squares are cut.
Suppose n ( □ ) is the number of invalid quadrilaterals that contain at least the specified squares (for example, n ( A , C ) is the number of invalid quadrilaterals that contain the corner A and the hole C , which might also contain the corner B ), then by PIE , the total number of invalid quadrilaterals is n ( A ) + n ( B ) + n ( C ) − n ( A , B ) − n ( A , C ) − n ( B , C ) + n ( A , B , C )
Let's first look at n ( A ) . Note that we can construct quadrilaterals by choosing 2 squares in the grid as its opposite corner squares, with that in mind, if a quadrilateral's bottom-left corner square lies on A , then for this quadrilateral to be invalid, its opposite corner square must either not lie on the same row or column as A (since it will become a pentagon when A is cut) or lie exactly on A (since it would be just the corner square A itself, it will be cut into a triangle). Hence, the number of possible locations for its top-right corner square for the quadrilateral to be invalid is n ( A ) = ( 8 − 1 ) × ( 8 − 1 ) + 1 = 5 0
With similar reasoning, we can also conclude that n ( B ) = n ( A ) = 5 0 .
Now let's look at n ( C ) . Another way to construct quadrilaterals is by choosing two vertical lines and two horizontal lines from the grid as its edges. Thus for a quadrilateral to contain the hole C , its left edge must be on the left of C , its right edge must be on the right of C , its top edge must be above C , and its bottom edge must be below C . There are 4 vertical lines on the left of C , 5 vertical lines on the right of C , 5 horizontal lines above C , and 4 horizontal lines below C . Hence, n ( C ) = 4 × 5 × 5 × 4 = 4 0 0
Consider n ( A , C ) . To construct quadrilaterals of this type, fix its bottom-left corner square on A , and choose a location for its top-right corner square such that it is not on the left of C and is not below C . ∴ n ( A , C ) = 5 × 5 = 2 5
With similar reasoning, we can also conclude that n ( B , C ) = 4 × 4 = 1 6 .
Let's now consider n ( A , B ) and n ( A , B , C ) . It's easy to see that n ( A , B ) = n ( A , B , C ) = 1 .
∴ n ( A ) + n ( B ) + n ( C ) − n ( A , B ) − n ( A , C ) − n ( B , C ) + n ( A , B , C ) = 5 0 + 5 0 + 4 0 0 − 2 5 − 1 6 − 1 + 1 = 4 5 9
The number of invalid quadrilaterals is 4 5 9 , therefore the number of quadrilaterals in the original grid is 1 2 9 6 − 4 5 9 = 8 3 7 .