The Shady Problem
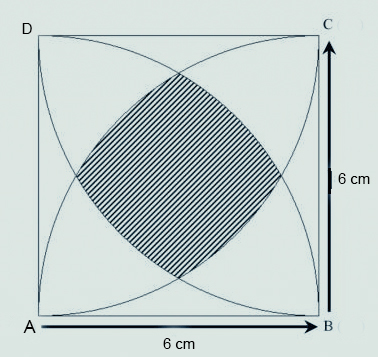ABCD is a square with sides of length 6 cm and it has 4 quadrants constructed from each of its vertices. Find the area of the shaded region.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
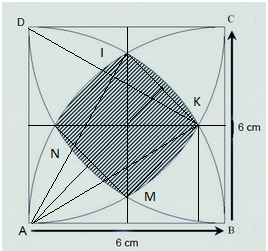Because:
∠
I
A
K
=
3
0
o
,
A
I
=
A
K
=
6
I
K
=
2
∗
S
I
N
(
1
8
0
π
∗
1
5
)
∗
6
=
3
.
1
S
(
⌢
I
K
)
=
1
2
π
∗
×
3
6
−
(
1
/
2
)
∗
3
6
∗
S
I
N
(
1
8
0
π
∗
3
0
)
=
0
.
4
2
4
S
s
h
a
d
e
d
=
I
K
2
+
4
∗
S
(
⌢
I
K
)
=
1
1
.
3
4
5
How is Angle IAK = 30 deg ?
Log in to reply
Let a point E be at the midpoint of A and B and another point F be at the intersection of line AB and the perpendicular of line AB going through point K . Triangle IAE is a 30-60-90 triangle with the 60 degree angle at IAE and triangle AKF is also a 30-60-90 with the 30 degree angle at KAF.
Since IAE is made up of angles IAK and KAF, we have
- IAE = IAK + KAF
- IAK = IAE - KAF
- IAK = 60 - 30 = 30
Log in to reply
u could also use similarity of triangles to prove that angle was trisected
What does symBol * means
In the first figure, arc ab =1/3 of arc DabB. Hence, angle aAb= 1/3 of angle DAB =30
So, angle Aab=angle Aba=(180-30)/2=75
Now, at triangle Aab: ab/sin30 = Aa/sin75=Ab/sin75 {Ab=Aa= 6cm}
Hence, ab= (6
sin30/sin75)= 3.1058 cm
Now, area of abcd square = (ab)^2= 9.646 cm^2 ..............................................................(i)
Again, in 2nd figure; area of shaded region= total area- area of Aab triangle
=(30/360)
pi6^2- 9
=3
pi- 9
=0.424778 cm^2 .............................(ii)
Finally : Total shaded area= (i)+4
(ii)
=9.646+1.699 cm^2
=11.345 cm^2
Poniżej brak jest objaśnienia,dlaczego kat IAK= 30 stopni ?