The Shortest Distance Between 2 Points On The Earth

Fix a point to find the average distance of the other points from it. Take the point as $A$ and centre $O$ . Consider another point $B$ on the surface. Let $\angle AOB = \theta$ . $\overline{AB} = 2 \sin \left ( \frac {\theta}{2} \right)$ with band radius $\sin \theta$ . So the average distance is

$\begin{aligned} 6378 \cdot \frac {1}{4\pi} \displaystyle \int_0^{\pi} (2 \pi \sin \theta ) \cdot 2 \sin \left ( \frac {\theta}{2} \right ) \mathrm{d} \theta & = & \displaystyle 6378 \cdot \int_0^{\pi} 2 \left ( \sin^2 \frac {\theta}{2} \right ) \cos \left ( \frac {\theta}{2} \right ) \mathrm{d} \theta \\ & = & \displaystyle 6378 \cdot 4 \int_0^1 y^3 \mathrm{d} y, \text{ let } y = \sin \frac {\theta}{2} \\ & = & 6378 \cdot \frac {4}{3} = \boxed{8504} \\ \end{aligned}$

In short, the average distance between two points of a sphere with radius $r$ is $\frac {4r}{3}$

Alternatively, consider a unit sphere which satisfy the equation $x^2+y^2+z^2=1$ . Without loss of generality, fix one point to be $(1,0,0)$ while the other is $(X,Y,Z)$ . the distance is $\sqrt{ (1-X)^2+Y^2+Z^2} = \sqrt{2-2X}$ , so the average is $\displaystyle \frac {1}{2} \cdot \int_{-1}^1 \sqrt{2-2X} \mathrm{d}X = \frac {1}{4} \int_0^4 \sqrt{w} \space \mathrm{d} w = \frac {4}{3}$ . In this case, multiply it by $6378$ and you should get the same answer.

For further reading, you may refer to this

$$ Let $A$ and $B$ be the two points that are uniformly and randomly chosen on the surface of the earth. Let $d$ be the straight line distance between $A$ and $B$ . See the picture below.

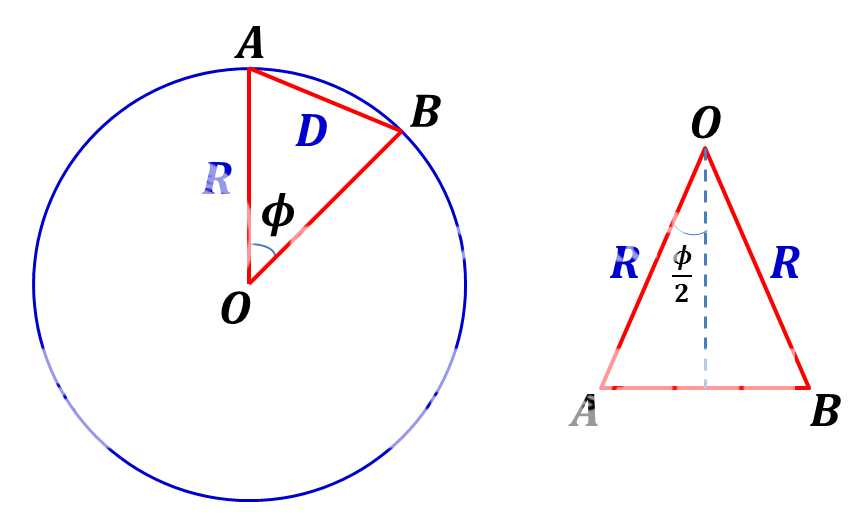Circle Intersection of Earth

Using $\Delta\text{ABO}$ , $\text{D}$ can easily be determined. $$ $d=2R\sin\left(\frac{\phi}{2}\right).$ $$ In this case, there are three random variables, namely: $\text{D},\Phi,$ and $\Theta$ . $\text{D}$ is the straight line distance between $A$ and $B$ , $\Phi$ is the polar or zenith angle from the positive $z$ -axis with $0\le\phi\le\pi$ , and $\Theta$ is the azimuthal angle in the $xy$ -plane from the $x$ -axis with $0\le\theta<2\pi$ .

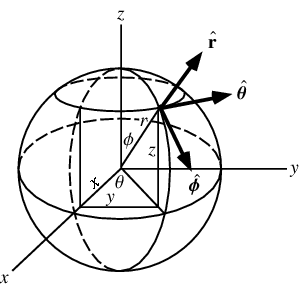Spherical Coordinates

Assuming that $\Phi$ and $\Theta$ are independent, the joint density function (pdf) of $\Phi$ and $\Theta$ turns out to be $$ $f_{\Phi,\Theta}(\phi,\theta)=f_{\Phi}(\phi)\cdot f_{\Theta}(\theta)$ $$ where $$ $f_{\Phi}(\phi)=\frac{1}{2}\sin\phi$ and $f_{\Theta}(\theta)=\frac{1}{2\pi}.$ $$ Thus, the average distance or expectation value of $\text{D}$ is $$ $\begin{aligned} \text{E}[\text{D}]&=\int_{\theta=0}^{2\pi}\int_{\phi=0}^{\pi}d\cdot f_{\Phi,\Theta}(\phi,\theta)\;d\phi\,d\theta\\ &=\int_{\theta=0}^{2\pi}\int_{\phi=0}^{\pi}2R\sin\left(\frac{\phi}{2}\right)\cdot f_{\Phi}(\phi)f_{\Theta}(\theta)\;d\phi\,d\theta\\ &=2R\int_{\theta=0}^{2\pi}\int_{\phi=0}^{\pi}\sin\left(\frac{\phi}{2}\right)\cdot \frac{1}{2}\sin\phi\cdot\frac{1}{2\pi}\;d\phi\,d\theta\\ &=\frac{R}{2\pi}\int_{\theta=0}^{2\pi}\;d\theta\int_{\phi=0}^{\pi}\sin\left(\frac{\phi}{2}\right)\sin\phi\;d\phi\\ &=\frac{R}{2\pi}\cdot2\pi\int_{\phi=0}^{\pi}\sin\left(\frac{\phi}{2}\right)\cdot2\sin\left(\frac{\phi}{2}\right)\cos\left(\frac{\phi}{2}\right)\;d\phi\\ &=2R\int_{\phi=0}^{\pi}\sin^2\left(\frac{\phi}{2}\right)\cos\left(\frac{\phi}{2}\right)\;d\phi\\ &=2R\int_{\phi=0}^{\pi}\sin^2\left(\frac{\phi}{2}\right)\cdot2\;d\left(\sin\left(\frac{\phi}{2}\right)\right)\\ &=4R\cdot\left.\frac{1}{3}\sin^3\left(\frac{\phi}{2}\right)\right|_{\phi=0}^\pi\\ &=\frac{4}{3}R\\ &=\frac{4}{3}\cdot6378\\ &=\boxed{\color{#3D99F6}{8504\text{ km}}} \end{aligned}$ $$

$\text{\# }\mathbb{Q.E.D.}\text{ \#}$