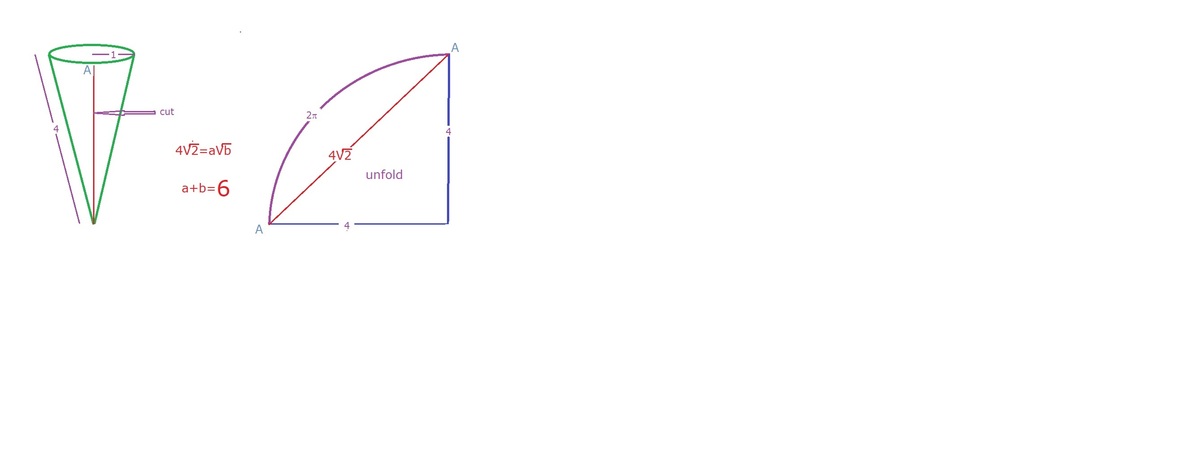
The shortest distance might go the long way round!

Consider you start cutting the cone from a point on the rim towards the the tip of the cone (You can't cut ice cream cones but I have special ones). You can expect that you will get a circle with a missing section in it. Now as the slant height is 4m the radius of the circle 4m. And the length of the arc becomes the circumference of the rim of the cone. $Circumference\quad of\quad the\quad rim=2\pi *1=2\pi \\ Angle\quad made\quad by\quad th\quad section\quad of\quad circle=\frac { 2\pi }{ 4 } radians=90degrees\\ We\quad know\quad apply\quad pythagoras\quad theorem\quad to\quad get\quad our\quad shortest\quad distance=\sqrt { { 4 }^{ 2 }+{ 4 }^{ 2 } } \\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad =4\sqrt { 2 } \\ Hence\quad answer\quad is\quad 6\\$