The Shortest Path

Computer Science Level 2

True or false :

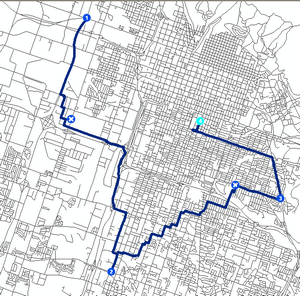
Given a weighted graph, the shortest path from a source to a destination is calculated using the shortest path algorithm. If the weight of every edge is increased by one, the shortest path will necessarily remain the same.

True False

2 solutions

Daniel Liu
Mar 31, 2016

Consider the following: Imgur Imgur

As it stands, the blue path is shorter than the red path. However, after incrementing everything two times, the red path becomes shorter than the blue path.

Maybe this isn't the best example since you increase by 1 twice. How about 1, 1, and 2.5?

Eli Ross Staff - 4 years, 7 months ago

Yep, that works. Using my construction, so does 0.5, 0.5 and 1.5.

Daniel Liu - 4 years, 7 months ago

Tyler Harmon
Mar 25, 2016

An example of a case where incrementing the weight of everything by one yields a more efficient route:

Assume you start at point A, and need to get to point B. There are two paths. Path A has 5 segments, each of which have weight of 1, so the total path weight is 5. Path B has 3 segments, each of which have a weight of 2, so the total path weight is 6.

Currently, path A will be taken. However, if all segments are incremented by 1, then path A becomes $5 \times 2 = 10$ , and path B becomes $3 \times 3 = 9$ , so the preference has shifted from path A to path B.

The Shortest Path

2 solutions

0 pending reports