The shortest trip
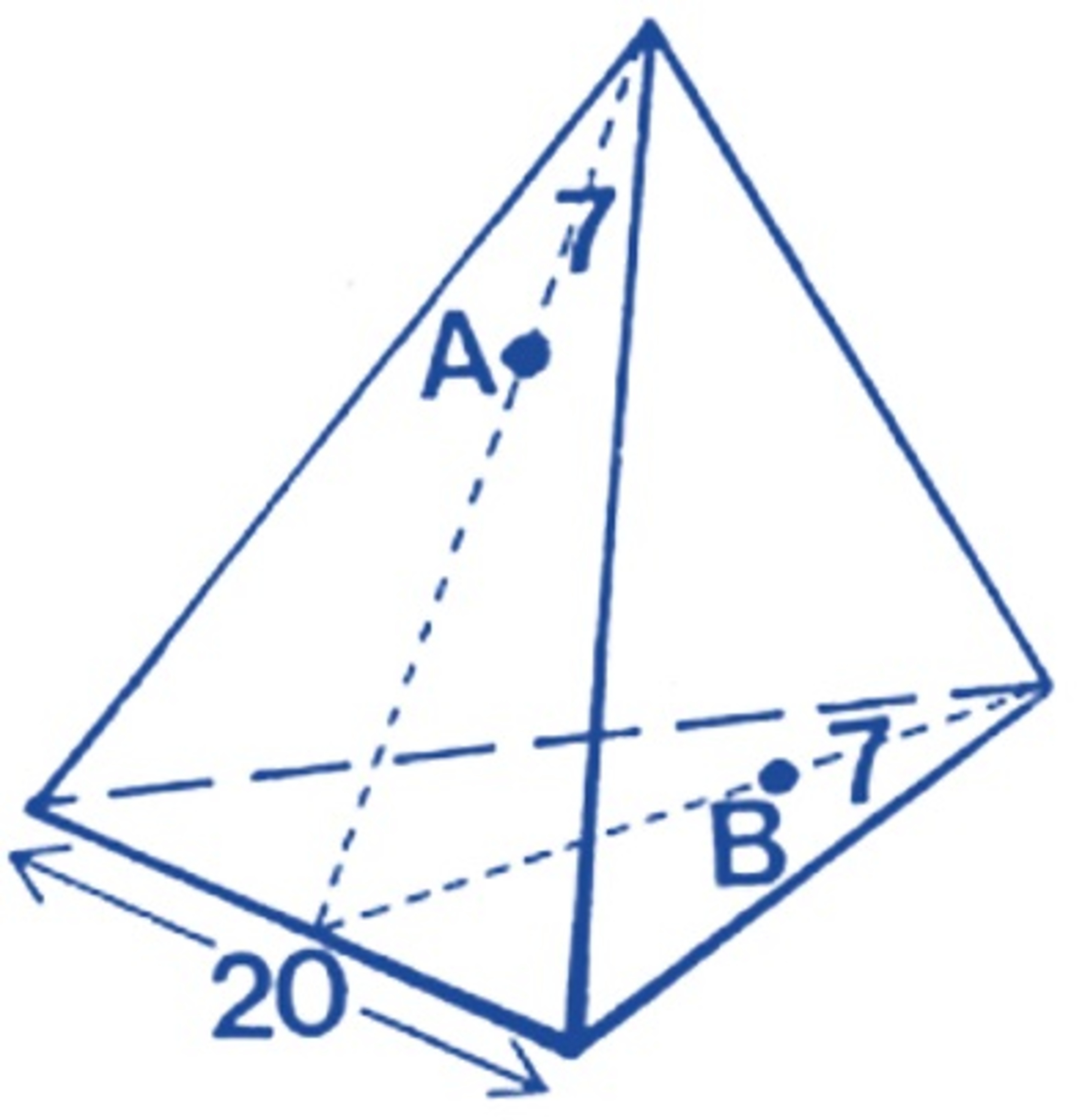
Within a room in the form of a regular tetrahedron, an ant moves from point A to B .
The room measures 20 meters on the side and each point is 7 meters from a vertex (distance is taken on the height of the triangular wall).
How long is the shortest path for the ant?
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
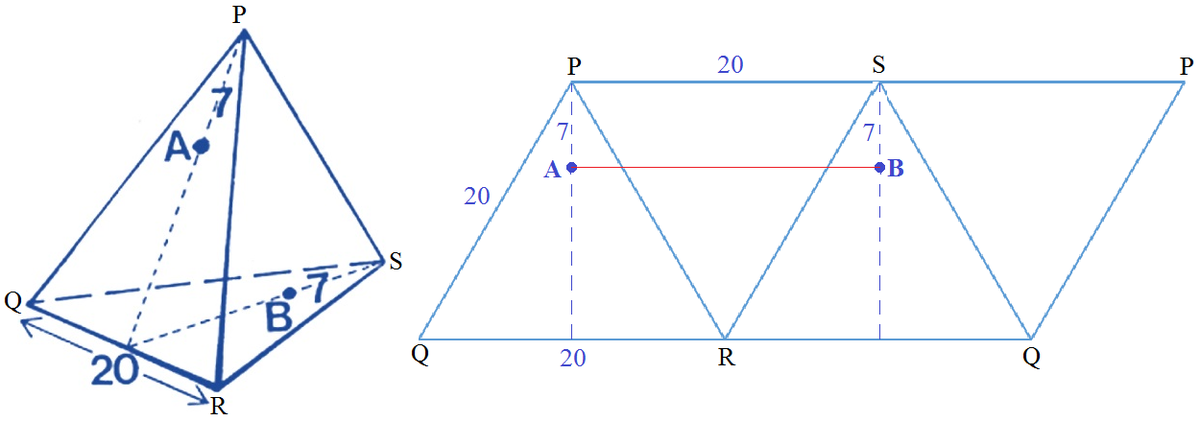Cut open the regular tetrahedron and lay the four surfaces flat. The shortest path from point
A
to
B
is the straight line joining them on the flat surface. We note the line
A
B
is parallel to and same length with
P
S
=
2
0
meters.