The Shrinking Square
Geometry
Level
5
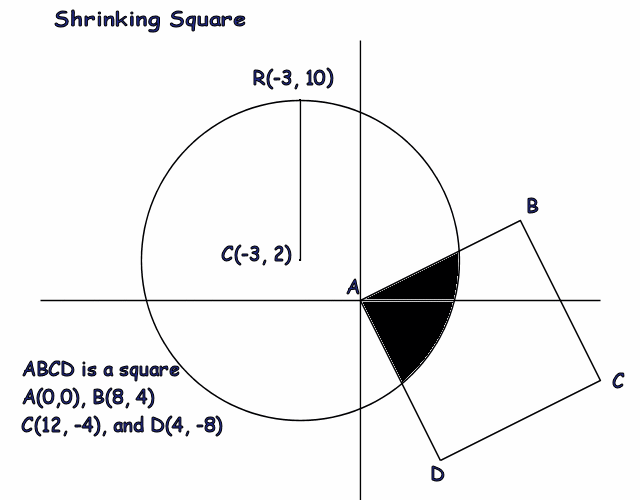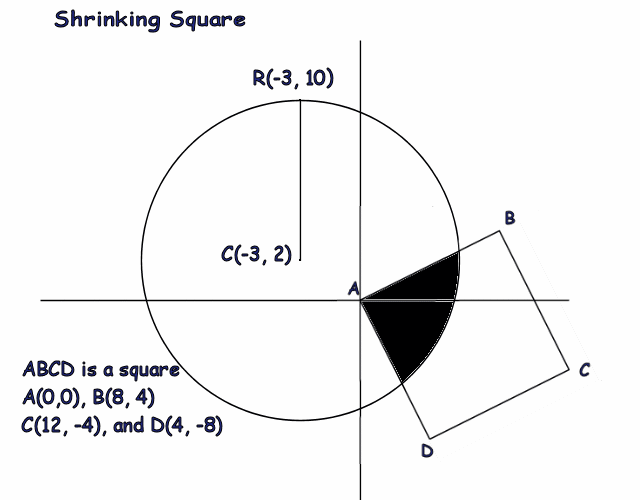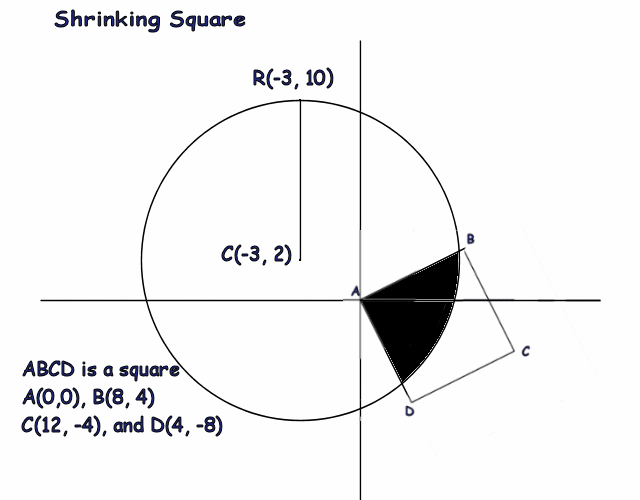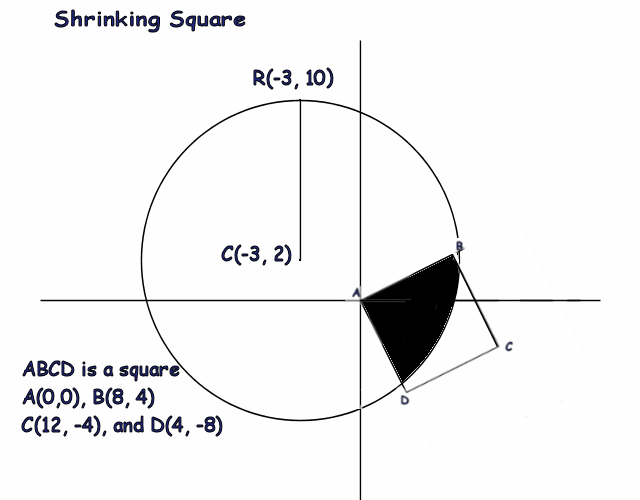 Find the length of a side of the square, (to nearest 3 decimals), when its intersection with the circle is exactly 1/2 of its area.
Find the length of a side of the square, (to nearest 3 decimals), when its intersection with the circle is exactly 1/2 of its area.
The answer is 5.88.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Here are outlines of two possible methods, one with integration and one without ....
(i) To make integration easier, rotate the circle and square counterclockwise about O an angle of arctan ( 2 ) radians so that side A D is horizontal and side A B is vertical. Under this rotation the coordinates of A then become
A ′ ( 0 . 1 3 0 4 9 5 1 , 3 . 7 8 8 8 5 4 5 ) = A ′ ( a , b ) .
Now look at the area of the region inside the circle that is above y = b and to the right of x = a . Now the line x = a intersects the circle at
P ( a , 9 . 3 6 2 0 6 ) = P ( a , c ) ,
and the line y = b intersects the circle at
Q ( 4 . 7 9 7 4 4 , b ) = Q ( d , b ) .
The area of this region is then
∫ a d ( 6 4 − ( x + 3 ) 2 + 2 − b ) d x = 1 7 . 2 8 5 5 .
Now note that the maximum of ( c − b ) and ( d − a ) is 5 . 5 7 3 2 2 5 5 , which when squared is 3 1 . 0 6 0 8 4 2 , which is less than half the area of the region calculated above. This indicates that both sides of the desired square must extend beyond the circle. This in turn means that the area calculated above will be half the area of the desired square, and hence the side length of said square will be
2 ∗ 1 7 . 2 8 5 5 = 5 . 8 7 9 7 to 4 decimal places.
(Edit: This is the graph of the (rotated) solution square.)
For the second method we won't need to rotate the diagram. By a similar argument as above, we can conclude that the sides of the desired square will extend beyond the circle. Labeling as R and S the respective points of intersection of sides A B and A D with the circle, we then need to subtract the areas of triangles Δ O A R and Δ O A S from that of sector O R S to obtain the area of region A R S . Once found, we then proceed as before by doubling this value and taking its square root to find the side length of the desired square. This involves the determination of the coordinates of points R and S , distances A R and A S , angles ∠ A O R and ∠ A O S , areas of the two triangles using Heron's formula and the area of the sector using the formula ( 2 1 ) ∗ 8 2 ∗ ( ∠ A O R + ∠ A O S ) , This is laborious but straightforward, and seeing that I've been typing for some while I will leave it to the reader to confirm that this will return the same value for the side length of the desired square. (It does, I assure you. :) )