The Slope and Concavity of the Area Between Two Functions

Calculus Level 4

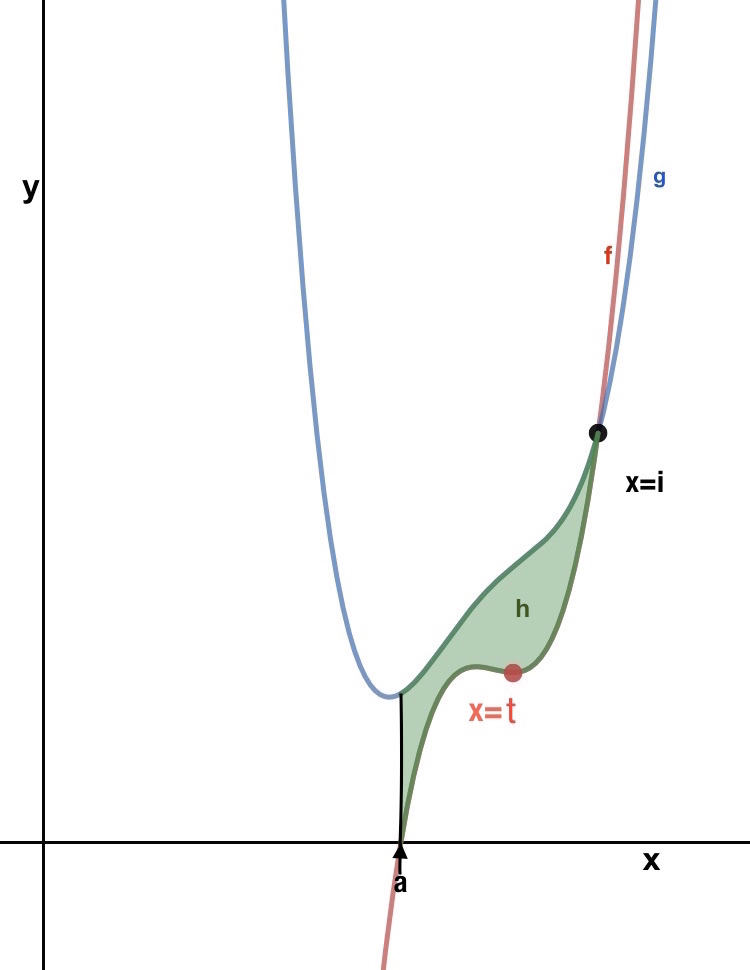
$g(x)$ is shown in blue. $f(x)$ is shown in red. $h(a)$ is represented by the green area between $g$ and $f$ .

Let $f, g, h$ be continous and differentiable functions. Let $h$ be defined as a function of $a$ such that

$h(a)= \int_{a}^{i} g(x)-f(x) dx$ .

$x=i$ is a point of intersection for $f$ and $g$ . $x=t$ is a critical point of $f$ .

Which of the following choices properly arranges the values of $h'$ and $h''$ from least to greatest?

(Ignore the answer choice " $h''(i)<h$ ")

h''(i)<h

h''(t)<h''(i)<h'(i)

h''(t)<h'(i)<h''(i)

h'(i)<h''(i)<h''(t)

1 solution

Zachary Stewart
Jul 2, 2018

$h'(a)= -(g(a)-f(a))$

$= f(a)-g(a)$

$h''(a)= f'(a)-g'(a)$

$h''(t)= f'(t)-g'(t)$

$= 0-g'(t)$

Because $g'(t)$ is positive ( $g$ is increasing at $x=t$ ), $h''(t)$ is negative.

$h'(i)= f(i)-g(i)$

$=0$

$h''(i)=f'(i)-g'(i)$

Both $f'(i)$ and $g'(i)$ are positive, but in the graph, we can see that $f$ is steeper than $g$ at $x=i$ and thus has a larger derivative at $x=i$ . This means that $h''(i)$ is positive.

In the proper order, $h''(t)$ , $h'(i)$ , $h''(i)$ .

The Slope and Concavity of the Area Between Two Functions

1 solution

0 pending reports