The sound of steel rods

When the first rod makes contact with the second rod, a compression wave begins to move at the speed of sound from the colliding end to the far end, and is then reflected back. The time required for the wave to travel the length of the rod twice, which is the duration of the collision event, equals $\frac{2l}{c} = \frac{0.6}{5000} = \textbf{0.00012}$ seconds.

As soon as the rods collide, a longitudinal pulse start traveling into the rods. The rods will go apart as soon as this pulse comes back to the point of contact after traversing the length of the rod twice. Thus, the collision lasts for a time $= \frac{0.6}{5000} = 0.00012$

We use Conservation of Momentum and Energy since the collision is elastic. We obtain a system with two equations and two unknowns to find the speed of the rebounded rod.

Then, from the obtained speed, the speed of the rod, and the length, we divide to find the time. We get $\fbox {1.2 E -4 s}$ .

T = 2L/c

T = 2 (0.3 m) / (5000 m/s)

T = 0.00012 seconds

Two identical moves with equal speed in opposite direction longitudinally. The key is to go to a frame of reference such that the other rod is fix and the other rod will double its length and speed because the rod is in the opposite direction then it follows that the length of each rod are additive. Therefore, in that frame the rod will seems to be longer.

t = 2(length of each rod) / (the speed of sound)

= 2 (0.3 m) / (5000 m/s)

t = 0.00012 sec

And also the speed of sound is control by the medium, which only depends on the properties of the materials and temperature. Therefore, the speed of sound for this problems doesn't depend on the choice of frames.

When the rods hit each other, a compression wave propagates at the speed of sound to the end of each rod and bounces back. When it returns, the rods separate. How long does that take? distance / rate = time $\Rightarrow$ 60 cm / 5000 m/s = 1.2e-4 s.

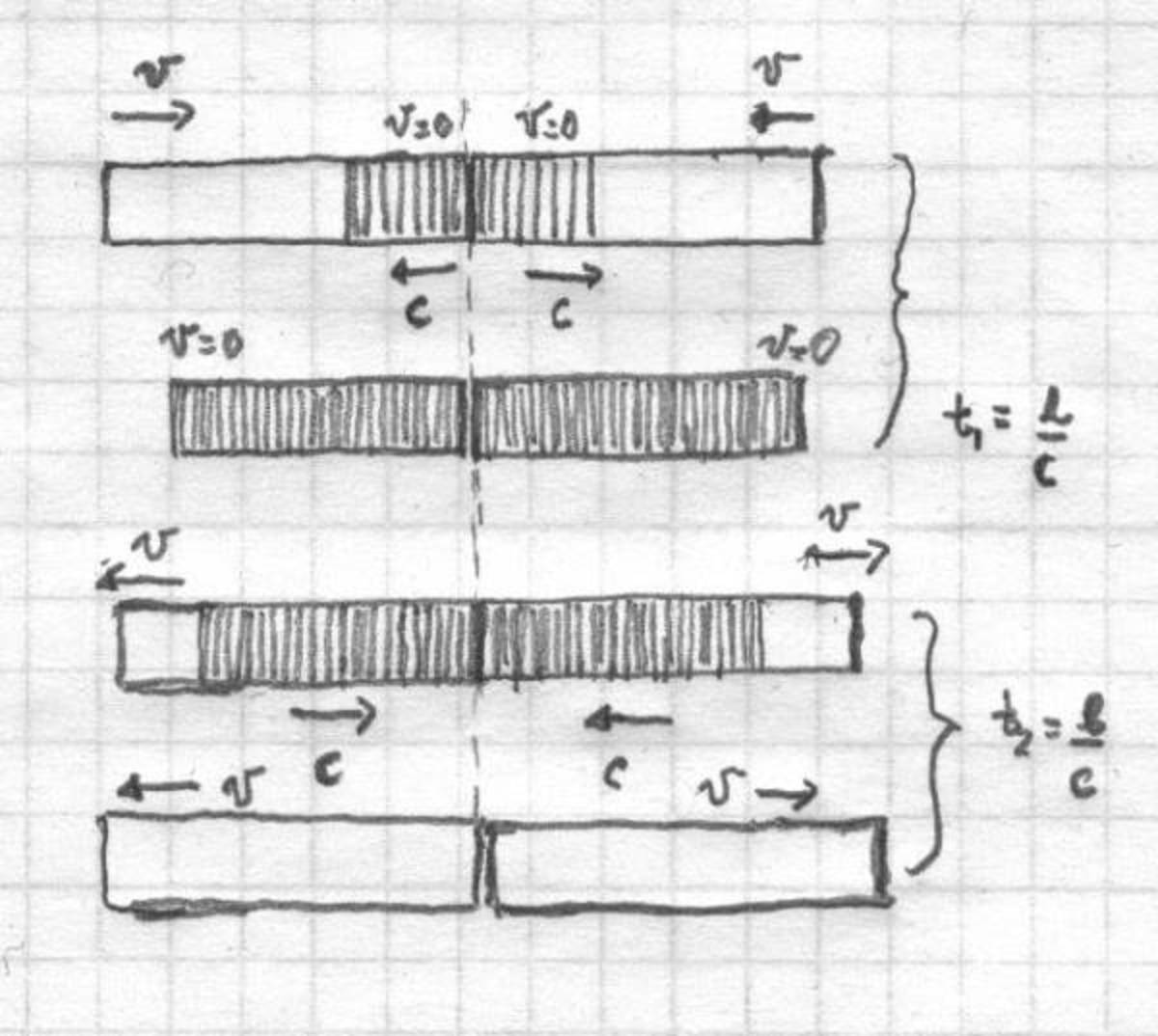
Right after the rods come into contact, neither of the free ends is aware of the collision until the compression wave reaches them (see the figure below). The information of the collision propagates with the speed of sound $c=5000 ~\mbox{m/s}$ . Thus, after $t_{1}=\frac{l}{c}$ the rods are entirely compressed (all the points have $v=0$ ). Now, the decompression wave starts propagating in the opposite direction. After the time $t_{2}=\frac{l}{c}$ the rods separate. Therefore, the collision lasts $t=t_{1}+t_{2}= \frac{2l}{c}= 1.2\times 10^{-4} ~\mbox{s}.$