The Special Point in a Triangle 2
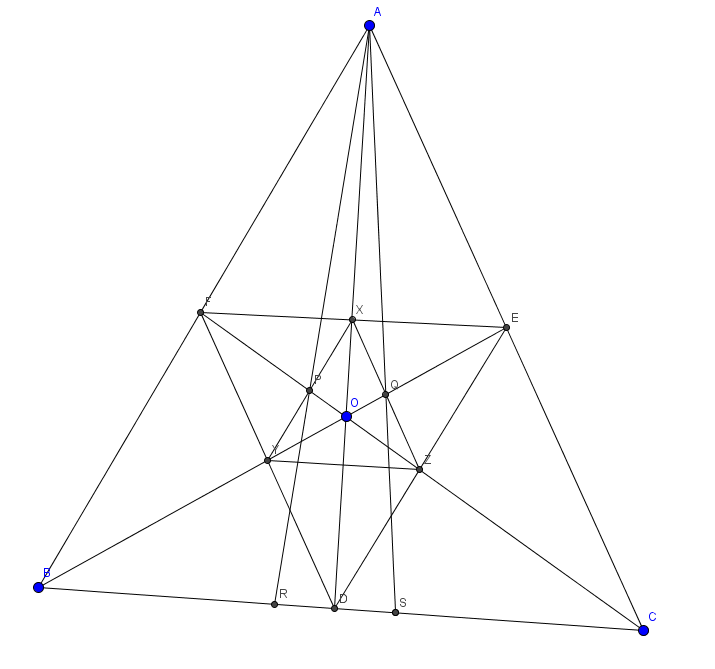
Let be a point in acute-angle triangle .
is the intersection of and . are defined similarly.
is the intersection of and . are defined similarly.
Let be the intersection of and and be the intersection of and .
is the intersection of with and is the intersection of with .
When is the circumcentre , .
When is the orthocentre , .
Find where we measure the angles in degrees.
Note : Where intersections between sides are described it is assumed the sides are extended if necessary.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Solution using areal coordinates:
Let A = ( 1 , 0 , 0 ) , B = ( 0 , 1 , 0 ) , C = ( 0 , 0 , 1 ) , O = ( l , m , n ) then we have: D = ( 0 , m , n ) , E = ( l , 0 , n ) , F = ( l , m , 0 )
The line A D has equation y n − m z = 0 and E F has equation − x n m + y n l + z l m = 0 . It follows that X = ( 2 l , m , n ) is on both lines. Symettrically, we have Y = ( l , 2 m , n ) , Z = ( l , m , 2 n ) .
The line X Y has equation − m n x − n l y + 3 m l z = 0 and C F has equation − x m + y l = 0 . Again, P = ( 3 l , 3 m , 2 n ) is on both of these lines. By symmetry, Q = ( 3 l , 2 m , 3 n ) .
It follows then that R = ( 0 , 3 m , 2 n ) , S = ( 0 , 2 m , 3 n ) so R C B R = 3 m 2 n .
It is known that the circumcentre has coordinates ( s i n ( 2 A ) , s i n ( 2 B ) , s i n ( 2 C ) ) and the orthocentre: ( t a n ( A ) , t a n ( B ) , t a n ( C ) )
So 3 s i n ( 2 B ) 2 s i n ( 2 C ) = 9 4 3 ⇒ s i n ( 2 B ) s i n ( 2 C ) = 3 2 3 ⇒ s i n ( B ) c o s ( B ) s i n ( C ) c o s ( C ) = 3 2 3
And: 3 t a n ( B ) 2 t a n ( C ) = 3 2 3 ⇒ s i n ( B ) c o s ( C ) c o s ( B ) s i n ( C ) = 3
Multiplying these two gives: ( s i n ( B ) s i n ( C ) ) 2 = 3 6 = 2 ⇒ s i n ( B ) s i n ( C ) = 2
Putting this back into the first expression gives c o s ( B ) c o s ( C ) = 3 6
Combining c o s ( C ) = 3 6 c o s ( B ) ⇒ ( c o s ( C ) ) 2 = 3 2 ( c o s ( B ) ) 2 and s i n ( C ) = 2 s i n ( B ) ⇒ ( s i n ( C ) ) 2 = 2 ( s i n ( B ) ) 2 gives:
( c o s ( C ) ) 2 + ( s i n ( C ) ) 2 = 1 = 2 ( s i n ( B ) ) 2 + 3 2 ( c o s ( B ) ) 2 = 3 4 ( s i n ( B ) ) 2 + 3 2 ( c o s ( B ) ) 2 + ( s i n ( B ) ) 2 ) = 3 4 ( s i n ( B ) ) 2 + 3 2
⇒ 3 1 = 3 4 ( s i n ( B ) ) 2 ⇒ ( s i n ( B ) ) 2 = 4 1 ⇒ s i n ( B ) = 2 1 ⇒ ∠ B = 3 0 ∘ as A B C is acute.
s i n ( C ) = 2 s i n ( B ) ⇒ s i n ( C ) = 2 2 ⇒ ∠ C = 4 5 ∘
So ∠ B 4 × ∠ C = 3 0 1 8 0 = 6 .
I wonder if someone can come up with a more elegant solution.