The Speck Of Dust Returns

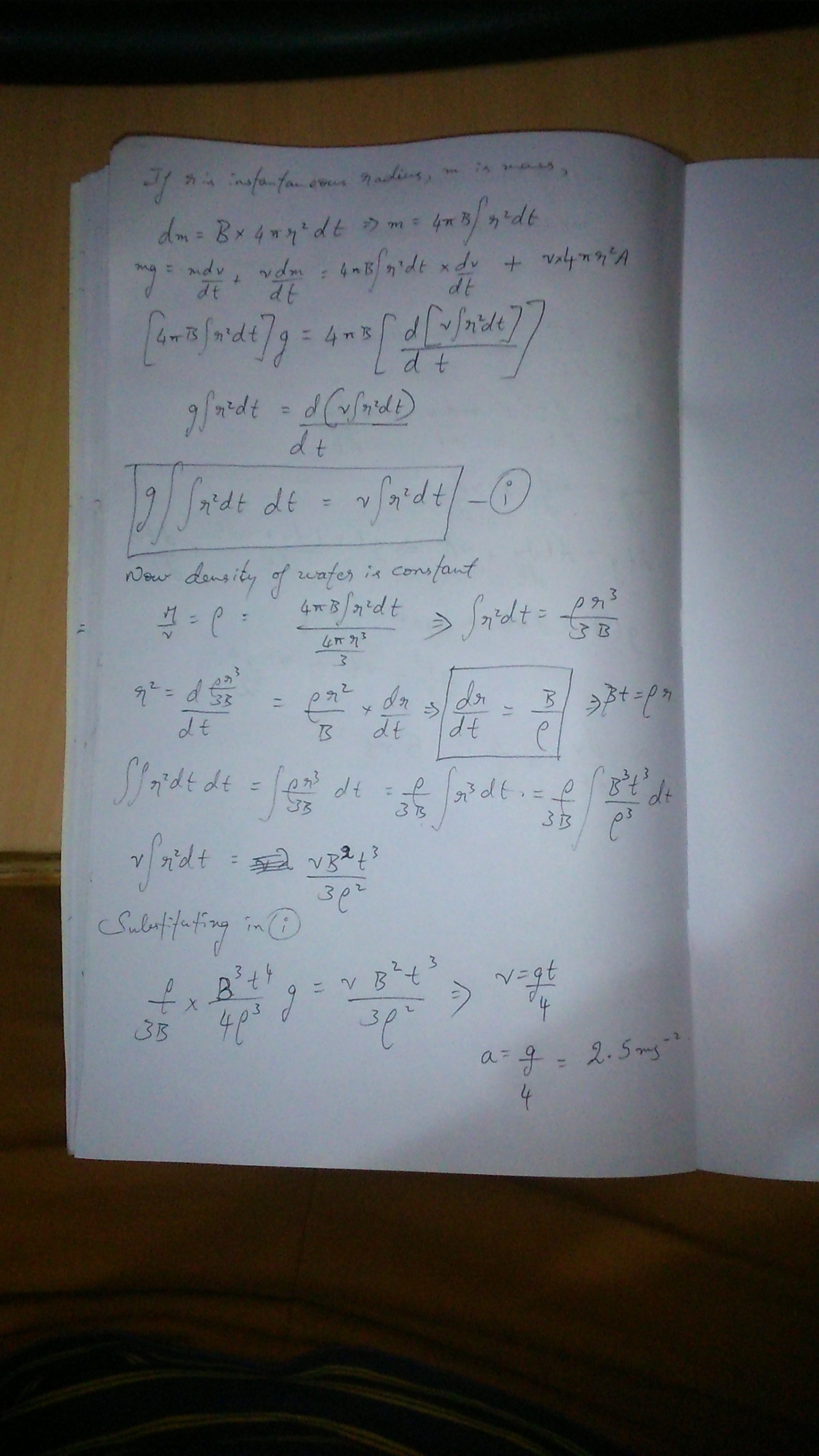
From the equation of motion (Newton's second law) we have: $mg = \frac{d}{dt}(mv)\;,$ with a time-dependent mass. We can recast the above equation as $\frac{dv}{dt} + \frac{1}{m}\frac{dm}{dt}v = g\;.$ Now we focus on the relative mass variation. According to the problem, we have: $\frac{dm}{dt} = BA\;,$ where $A$ is the drop surface. Being the latter spherical, $A = 4\pi r^2$ , with $r$ the radius of the drop. The mass of the drop can be written as $m = \frac{4\pi}{3}\rho r^3\;,$ where $\rho$ is the water density. Assuming the latter constant, we obtain $\frac{dr}{dt} = \frac{B}{\rho}\;.$ Assuming $B$ constant (it should be stated in the problem), we find the time evolution of the radius: $r = \frac{B}{\rho}t\;.$ We can put to zero the integration constant because the problem says that at the beginning the speck of dust has negligible mass. The latter is written then $m = \frac{4\pi B^3}{3\rho^2}t^3\;,$ so that $\frac{1}{m}\frac{dm}{dt} = \frac{3}{t}\;.$ The equation of motion becomes $\frac{dv}{dt} + \frac{3}{t}v = g\;,$ whose solution is $v = \frac{g}{4}t\;,$ where I used the initial condition $v(0) = 0$ . Deriving the velocity with respect to time we obtain the acceleration: $\boxed{a = \frac{g}{4}}$