The Sphere Floats And Sinks

Classical Mechanics Level 1

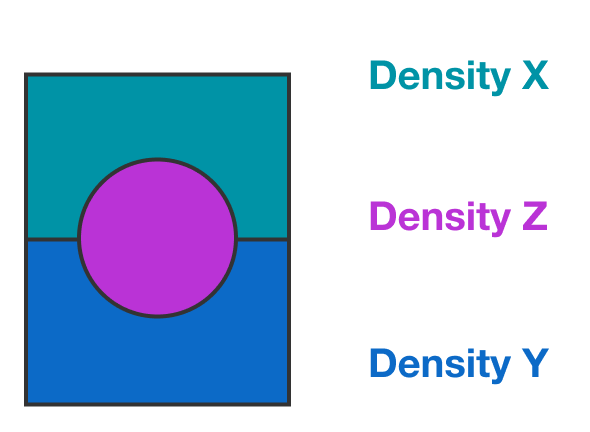
There are two liquids $A$ and $B$ of densities $X$ and $Y$ respectively. The liquids do not mix and $A$ floats on $B$ .

There is a sphere $C$ of density $Z$ which floats stably at the interface of liquids $A$ and $B$ , such that half of its volume is in $A$ , and the other half is in $B$ .

Which of the following gives the correct relationship between $X,Y$ and $Z?$

Z<X<Y

X < Y < Z

X < Z < Y

X = Y = Z

Z<Y<X

2 solutions

Sonia Gupta
Mar 27, 2016

It is first given in the question that $A$ & $B$ are of different densities so that $A$ floats on $B$ . So, $X < Y$ and $C$ is floating such that it is half in $B$ means it is floating above $B$ & is lighter than $B$ & floats half in A means it is heavier than $A$ . So, $X<Z<Y$ .

Abhiram Rao
Mar 26, 2016

As $A$ floats on $B$ , X is less than $Y$ . $C$ floats in such a way that half of its volume is in $A$ , and the other half is in $B$ . So, density of $C$ , $(Z) = X+Y/2$ , which is greater than $X$ but is less than $Y$ . Therefore , $X < Z < Y$ .

The Sphere Floats And Sinks

2 solutions

0 pending reports