The spring's mass isn't negligible?
Suppose you have a regular spring-mass setup, with the spring's fixed end at the origin of a Cartesian coordinate system and the free end is connected to a point-mass free to move along the -axis.
Let the total stretched length of the spring at any time be .
The point-mass moves at a velocity at an instant in time.
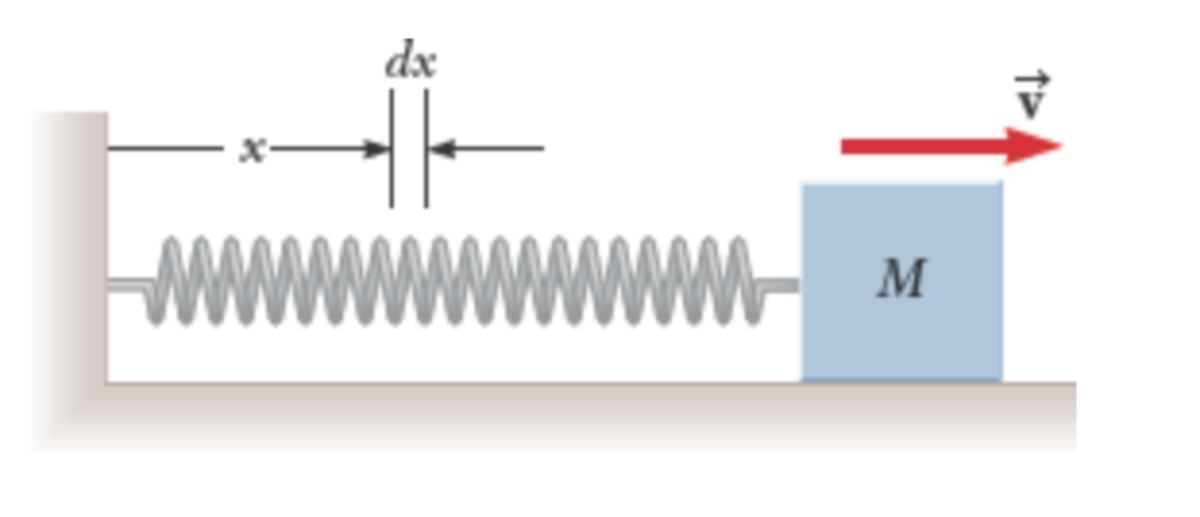
The spring is of mass lowercase and of uniform density.
If there is a mass element of length that is units away from the fixed end of the spring, .
The velocity of the same small mass element will be
Find the total kinetic energy of the system when the velocity of the point-mass is .
The answer comes in the form
Where are coprime positive integers.
Type your answer as .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the spring has mass and a uniform density, integrating each differential kinetic energy d T is the best approach.
d T = 2 1 u 2 d m
T s = ∫ m 2 1 u 2 d m
Where d m = L m d x , and u = L x v
T s = 2 1 L m ∫ 0 L ( L v x ) 2 d x
T s = 2 1 L 3 m v 2 3 L 3
This leaves the kinetic energy of the spring as 6 m v 2 . The rest is pretty straightforward, adding the kinetic energy of the mass to the expression.
The resultant expression is T ( v ) = 2 1 ( M + 3 1 m ) v 2