The Square-Circle Problem
Suppose we have a square ABCD and we draw a circumference which goes through point A and the middle points of the sides BC and CD.
Which has the biggest perimeter?
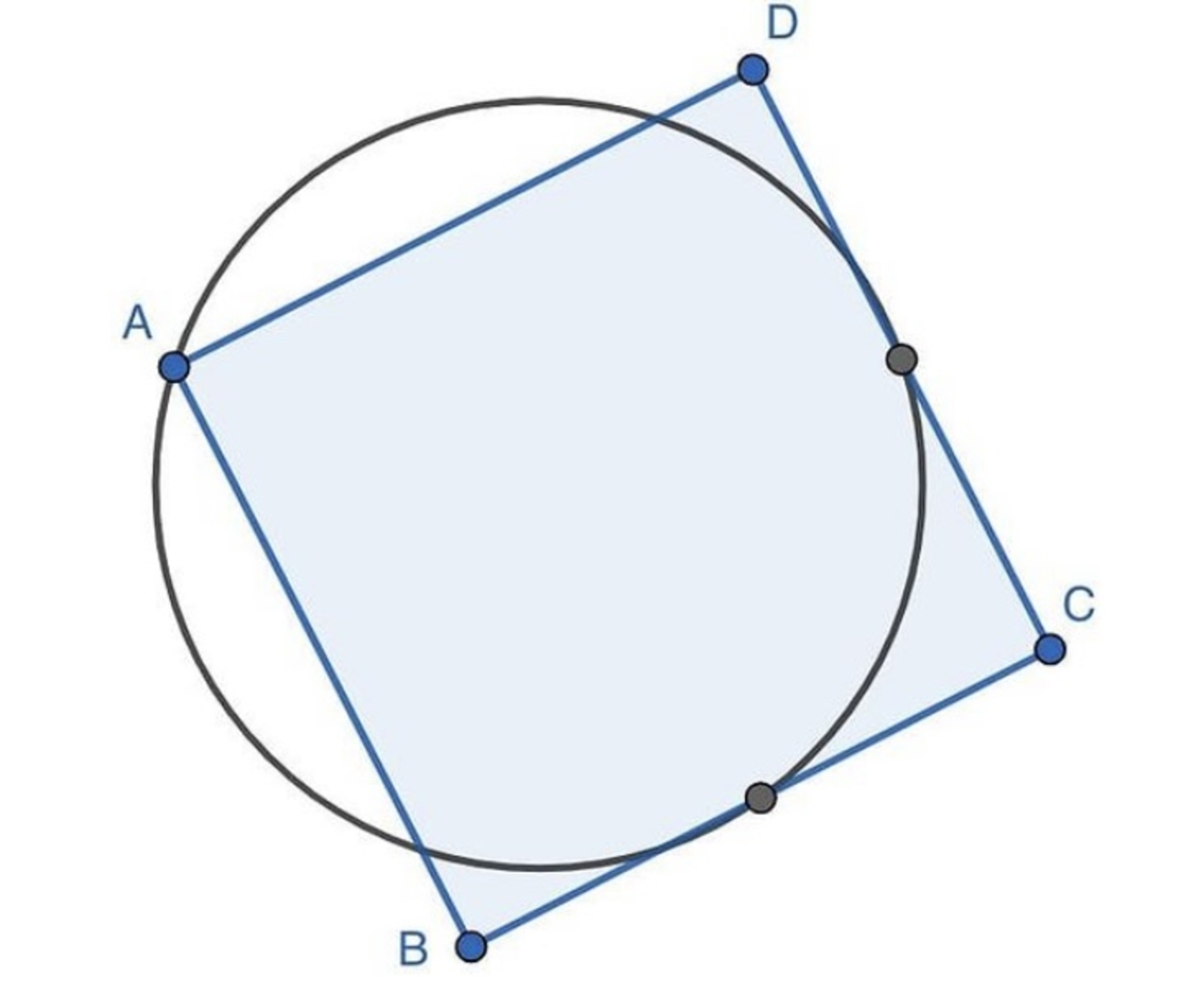
Extra problem: Which has the biggest area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Fantastic solution, you are so brilliant. A pure geometric solution. I love it! ❤️
Suppose we draw a square ABCD centered on the cartesian plane where:
A = ( − 1 , 1 ) ; B = ( − 1 , 1 ) ; C = ( 1 , − 1 ) ; D = ( 1 , 1 )
Notice that each side of the square has distance 2. Then, we can say:
P s q u a r e = 4 ⋅ 2 = 8
We can calculate the middle points of the side BC and CD:
I will denote M : = middle point of BC ; N : = middle point of CD
M = ( 0 , − 1 ) ; N = ( 1 , 0 )
Also, we know a circumference goes trough points A , N and M
Therefore, grafically we have the following situation:
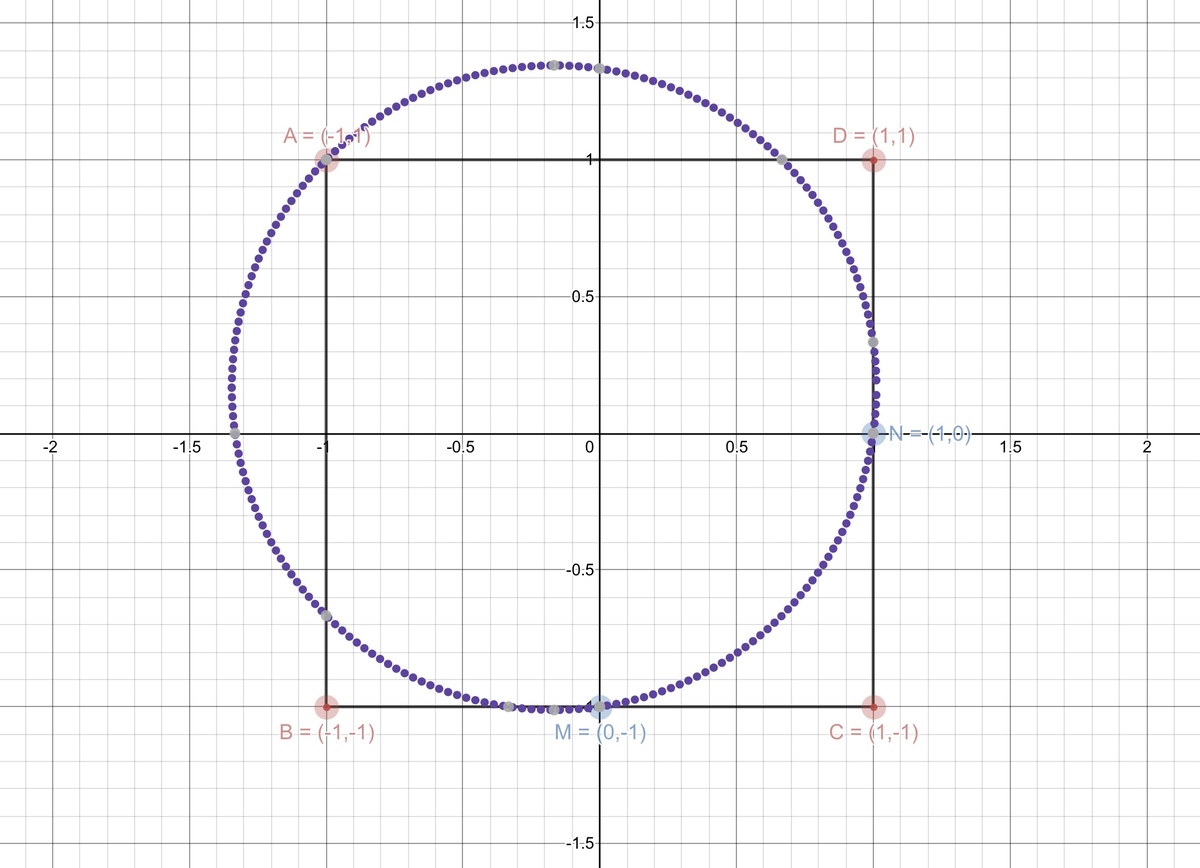
The equation of any circumference can be expressed as: ( x − a ) 2 + ( y − b ) 2 = r 2 , where the point ( a , b ) is the center and r is the radius.
Notice that circumference goes through points A = ( − 1 , 1 ) , N = ( 1 , 0 ) and M = ( 0 , − 1 ) . Then, this 3 points satisfy the previous equation. Therefore, we have:
( 1 ) —> ( − 1 − a ) 2 + ( 1 − b ) 2 = r 2
( 2 ) —> ( 1 − a ) 2 + ( − b ) 2 = r 2
( 3 ) —> ( − a ) 2 + ( − 1 − b ) 2 = r 2
Using ( 2 ) and ( 3 ) :
( 2 ) —> ( 1 − a ) 2 + ( − b ) 2 = r 2 ⟹ 1 − 2 a + a 2 + b 2 = r 2
( 3 ) —> ( − a ) 2 + ( − 1 − b ) 2 = r 2 ⟹ a 2 + 1 + 2 b + b 2 = r 2
Equating ( 2 ) and ( 3 ) :
1 − 2 a + a 2 + b 2 = a 2 + 1 + 2 b + b 2 ⟹ 2 a + 2 b = 0 ⟹ a + b = 0
Using ( 1 ) and ( 2 ) :
( 1 ) —> ( − 1 − a ) 2 + ( 1 − b ) 2 = r 2 ⟹ 1 + 2 a + a 2 + 1 − 2 b + b 2 = r 2
( 2 ) —> ( 1 − a ) 2 + ( − b ) 2 = r 2 ⟹ 1 − 2 a + a 2 + b 2 = r 2
Equating ( 1 ) and ( 2 ) :
1 + 2 a + a 2 + 1 − 2 b + b 2 = 1 − 2 a + a 2 + b 2 ⟹ 4 a − 2 b + 1 = 0 ⟹ 4 a − 2 b = − 1 ⟹ 2 a − b = − 1 / 2
Now, using the two equations contained in boxes. We can calculate a and b using the reduction method:
a = − 1 / 6 ; b = 1 / 6
We know ( − 1 / 6 , 1 / 6 ) is the center of the circumference. Then, the circumference equation has the following form:
( x + 1 / 6 ) 2 + ( y − 1 / 6 ) 2 = r 2
Using the circumference goes through point A = ( 1 , 1 ) , for example. We can calculate the radius:
( − 1 + 1 / 6 ) 2 + ( 1 − 1 / 6 ) 2 = r 2 ⟹ r 2 = 5 0 / 3 6 ⟹ r = ( 5 2 ) / 6
Therefore, we can calculate the perimeter of the circumference:
P c i r c u m f e r e n c e = 2 π r = 2 ⋅ 3 . 1 4 ⋅ ( 5 2 ) / 6 = 7 . 4 0 4 . . .
Finally, we can conclude P s q u a r e > P c i r c u m f e r e n c e
Extra Problem
We have all the information calculated. We only need to calculate the areas:
A s q u a r e = 2 ⋅ 2 = 4
A c i r c u m f e r e n c e = π r 2 = 3 . 1 4 ⋅ ( 5 2 ) / 6 = 4 . 3 6 1 . . .
Finally, we can conclude A c i r c u m f e r e n c e > A s q u a r e
Geometric solution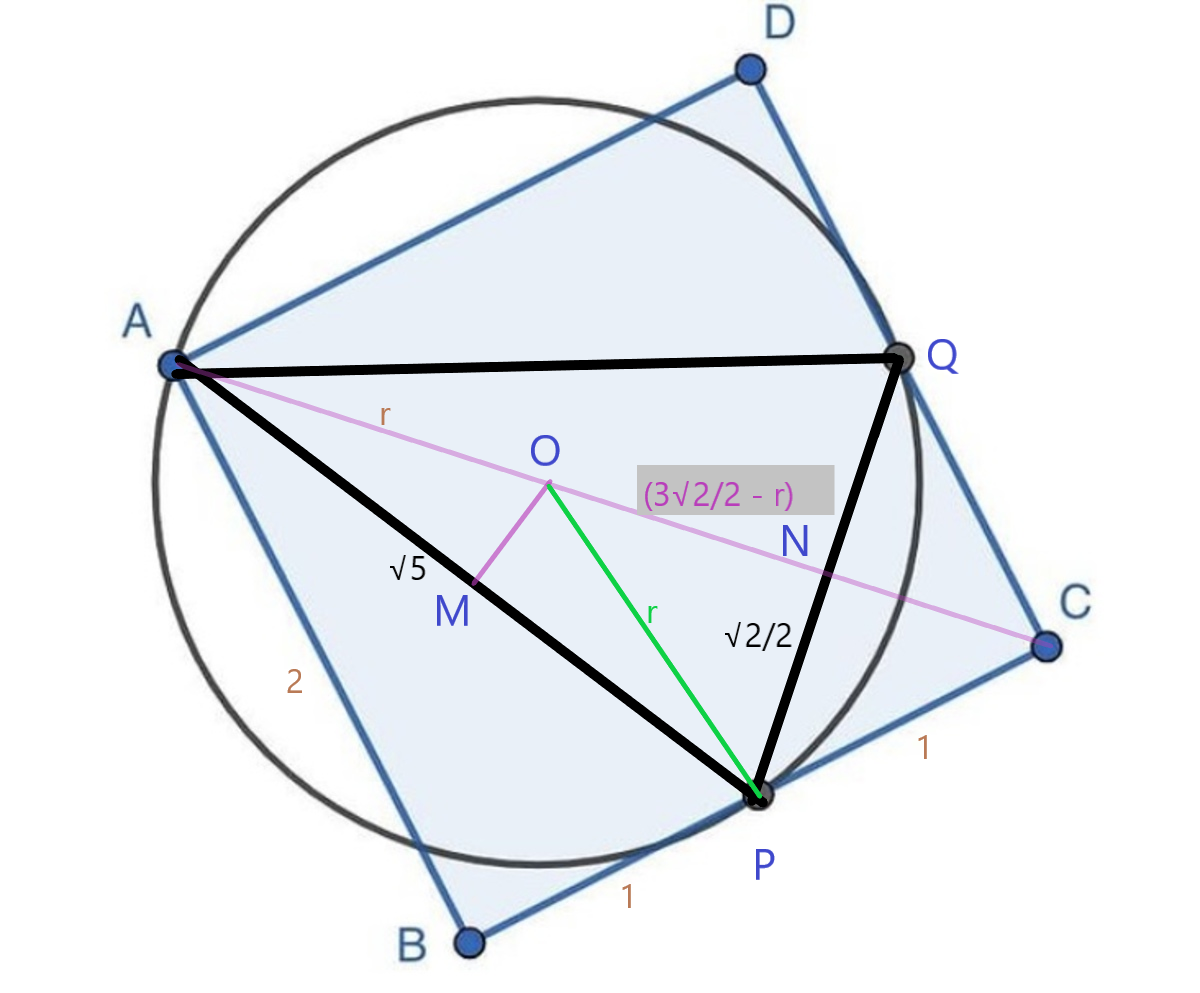
Let the side of the square = 2 units. Then AB = 2 and BP = 1, so AP = 5 . (pythagorean) Let the radius of the circle = r units. Then OA = OP = 2. Let M & N be the midpoints of AP & PQ respectively. The centre O of the circle can be found by drawing the right bisectors of AP and PQ at M & N. Note that since triangle PQC is a right isosceles triangle, PQ is perpendicular to diagonal AC and N is on the diagonal, so NO is on AC. Therefore AON forms a straight line. Since P Q = 2 (pythagorean), P N = 2 2 A N = A P 2 − P N 2 = ( 5 ) 2 − ( 2 2 ) 2 = 2 3 2 . O N = A N − A O = 2 3 2 − r . By Pythagorean, O P 2 = P N 2 + O N 2 ∴ r 2 = r 2 = 0 = r = ( 2 2 ) 2 + ( 2 3 2 − r ) 2 2 1 + 2 9 − 3 2 r + r 2 5 − 3 2 r 3 2 5 = 6 5 2 So the perimeter of the circle = 2 π r = 3 5 2 π ≈ 7 . 4 Since the perimeter of the square is 8, the square's perimeter is greater than the circle's perimeter.