The Stair Integral
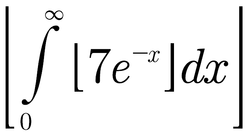 Evaluate.
Evaluate.
PS: Working towards a general result might help.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I use the definite integral definition and drawing the graph and abstract thinking, am.I right?
Even though I did not generalize yet I got the form from actual calculation. You did exactly as the question asked. Nice !!!
answer is 2
When x=0, 7 e − x =7, and it keeps decreasing.
Therefore, its graph would be a staircase with six stairs.
Horizontally cut the stairs, you end up with six rectangles, each with height being 1 and the top one being the smallest.
Just work out the width of each rectangle and sum them, the expression is − ln 7 6 − ln 7 5 − ln 7 4 − ln 7 3 − ln 7 2 − ln 7 1 = 5 . 1 . . . .
Consider the integral
I = ∫ 0 ∞ ⌊ n e − x ⌋ d x
Substituting n e − x = t we get:
I = ∫ 0 n t ⌊ t ⌋ d t
= r = 0 ∑ n − 1 ∫ r r + 1 t r d t
= r = 0 ∑ n − 1 r ln ( r r + 1 )
= r = 0 ∑ n − 1 ( r + 1 ) ln ( r + 1 ) − r ln ( r ) − r = 0 ∑ n − 1 ln ( r + 1 )
The first sum is a telescopic sum. Evaluating the above summations we get:
I = ln ( n ! n n )
Substituting n = 7 we get ⌊ I ⌋ = 5