The story of a ball and a slope SJPO question
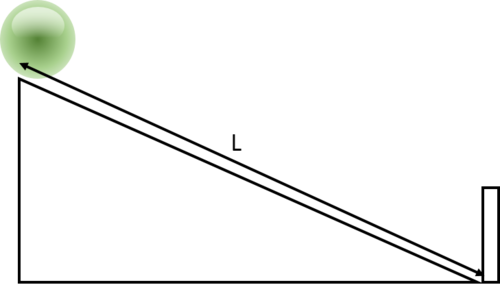 As shown in the figure above, a ball slides along a friction-less ramp of length
. As it reaches the bottom, it hits the board and slides up along the slope again, which it continues to do until it comes to rest.
As shown in the figure above, a ball slides along a friction-less ramp of length
. As it reaches the bottom, it hits the board and slides up along the slope again, which it continues to do until it comes to rest.
If the speed of the ball after the collision is times the speed of the ball just before the collision, find the total distance traveled by the ball when it comes to a complete stop.
The total distance traveled by the ball can be expressed as . What is ?
Extra fact : This is one of the easiest problems from the 2012 SJPO Special Round with a rating of only 5m.
This question is part of my set SJPO Practice Questions .
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
By using the formula for kinetic energy and gravitational potential energy, it can be seen that the kinetic energy is directly proportional to the height that the ball would rise:
2 1 m v 2 = m g h K E α h K E α v 2
So since the speed decreases to 5 4 after every collision, the kinetic energy and height decreases to 5 4 2 after every collision.
Since the ball is going to bounce until it stops, it is assumed to bounce infinity times, and the distance it travels is thus as:
2 ∑ n = 1 ∞ [ 5 4 ] 2 n + 1
Let ∑ n = 1 ∞ [ 5 4 ] 2 n be S
∑ n = 1 ∞ [ 5 4 ] 2 n − ∑ n = 2 ∞ [ 5 4 ] 2 n = [ 5 4 ] 2 = S − S [ 5 4 ] 2
Therefore, S = 9 1 6 which makes L [ 2 ∑ n = 1 ∞ [ 5 4 ] 2 n + 1 ] = 9 4 1 L
a + b = 4 1 + 9 = 5 0