The story of a peacock and a snake

Geometry Level 4

A peacock on a tree of 9 feet height on seeing a snake coming towards its hole situated just below the tree from a distance of 27 feet away from the tree flies to catch it. The peacock after catching it walks back to the hole. If they both possess the same speed, and the ratio of the total distance travelled by the peacock to the distance from the catching point to the tree is in the form of $\frac{a}{b}$ where $a$ and $b$ are co-prime integers, then find $a+b$

The answer is 13.

1 solution

Ashrit Ramadurgam
Mar 22, 2016

Let us visualize the problem: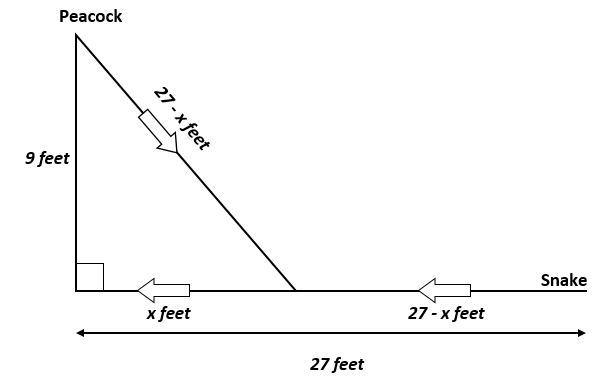 Let the distance from the tree to the catching point be $'x'$ feet. Then the distance travelled by the snake will be $(27-x)$ feet. Since the snake and the peacock possess the same speed, the distance flied by the peacock will also be $(27-x)$ feet.

Now by Pythagorean theorem, we have $(27-x)^2 = 9^2 + x^2$ $729 + x^2 - 54x = 81 + x^2$ $54x = 648$ $\boxed{x = 12}$ The total distance travelled by the peacock will be $(27-x) + x = 27$ feet $\frac{27}{12} = \frac{9}{4} = \frac{a}{b}$ Hence, $\boxed{a+b = 9 + 4 = 13}$

Short, simple approach. Up voted. Total distance traveled by the peacock may be taken directly as 27

I did it through geometry. It was a little long.
The steps were:-
Join peacock and snake points and draw perpendicular bisector to meet snake line at catching point. Solving similar right triangles and using Pythagoras Theorem we get distance traveled by snake alone as 12. This also the distance the peacock flied since the speed is same.

Niranjan Khanderia - 5 years, 2 months ago

Nicely written! +1!

Rishik Jain - 5 years, 2 months ago

Thanks Rishik Jain, and I liked your status ;)

Ashrit Ramadurgam - 5 years, 2 months ago

The story of a peacock and a snake

The answer is 13.

1 solution

0 pending reports