The Sum and the Square Meet

Probability Level 4

Mahoney chooses two real numbers that are on the closed interval [0,100] randomly, uniformly, and independently.

β¦Ώ He says that the two numbers are 𝘨𝘰𝘰π˜₯ if their sum is greater than at least one of their squares.

β¦Ώ He says that the two numbers are 𝘣𝘒π˜₯ if their sum is less than both of their squares.

β¦Ώ He says that the two numbers are 𝘧π˜ͺ𝘯𝘦 if their sum is equal to one or more of their squares.

What is the probability, rounded to the nearest thousandth, the two real numbers he chooses are good?


The answer is 0.144.

Maximilian Million Kenney by Maximilian Million Kenney , 13

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Chris Lewis
Jul 30, 2020

Let's call the two numbers x x and y y , and assume x ≀ y x\le y .

The pair ( x , y ) (x,y) is now good if x + y > x 2 x+y>x^2 , or y > x 2 βˆ’ x y>x^2-x .

We can plot this region in 2 2 -d:

The whole shaded area represents the region defined by x ≀ y x \le y , 0 ≀ x ≀ 100 0\le x \le 100 and 0 ≀ y ≀ 100 0\le y\le 100 . The blue areas are "good"; the grey area is "bad". (Note I've altered the scale here to highlight the detail in the bottom left corner.)

The dark blue area is a trapezium, with vertices at ( 0 , 0 ) , ( 2 , 2 ) , ( 2 , 100 ) , ( 0 , 100 ) (0,0),(2,2),(2,100),(0,100) . Its area is D = 198 D=198 .

The light blue area is defined by the lines x = 2 x=2 , y = 100 y=100 and y = x 2 βˆ’ x y=x^2-x .

To work out its area, we need to find where the parabola meets y = 100 y=100 ; this is just a quadratic: x 2 βˆ’ x = 100 x^2-x=100 , with solution x = 1 2 ( 1 + 401 ) x=\frac12 \left( 1+\sqrt{401} \right) .

We can now integrate to find the area: L = ∫ 2 1 2 ( 1 + 401 ) 100 βˆ’ ( x 2 βˆ’ x ) d x = [ 100 x βˆ’ 1 3 x 3 + 1 2 x 2 ] 2 1 2 ( 1 + 401 ) β‰ˆ 519.918 \begin{aligned} L&=\int_2^{\frac12 \left( 1+\sqrt{401} \right)} 100-\left(x^2-x \right) dx \\ &= \left[ 100x-\frac13 x^3 + \frac12 x^2 \right]_2^{\frac12 \left( 1+\sqrt{401} \right)} \\ &\approx 519.918 \end{aligned}

The probability of a "good" pair is therefore D + L 5000 β‰ˆ 0.14358 \frac{D+L}{5000}\approx \boxed{0.14358}

5 Helpful 2 Interesting 1 Brilliant 0 Confused

It looks like we got slightly different answers. How did you get 0.139 0.139 ?

Chris Lewis - 10Β months, 2Β weeks ago

Log in to reply

I got 401 401 + 585 60000 β‰ˆ 0.144 \frac{401\sqrt{401}+585}{60000} \approx 0.144 as well.

David Vreken - 10Β months, 2Β weeks ago

Thanks. I've updated the answer to 0.144 . Those who previously answered 0.144 has been marked correct.

Brilliant Mathematics Staff - 10Β months, 2Β weeks ago

We can call the numbers x and y. We know that: 0≀ x,y ≀100. Our goal is to find: P(x+y > xΒ² or x+y > yΒ²) Since P(x+y> xΒ²) and P(x+y>yΒ²) are independent events, and they are overlapping (they can both happen at the same time[ example: x=1, y=1]), the probability is:

P(x+y>xΒ² or x+y>yΒ²) = P(x+y>xΒ²) + P(x+y>yΒ²) - P(x+y>xΒ²)Β·P(x+y>yΒ²)

Notice that P(x+y>xΒ²) = P(y>xΒ²-x) and P(x+y>yΒ²) = P(x>yΒ²-y). P(y>xΒ²-x) is the same thing as P(x>yΒ²-y), just the variables are switched. So, the probability equation becomes:

P(x+y>xΒ² or x+y>yΒ²) = 2P(x+y>xΒ²) - P(x+y>xΒ²)Β²

Now find P(x+y>xΒ²)=P(y>xΒ²-x). We can graph 0≀ x,y ≀100 and y>xΒ²-x:

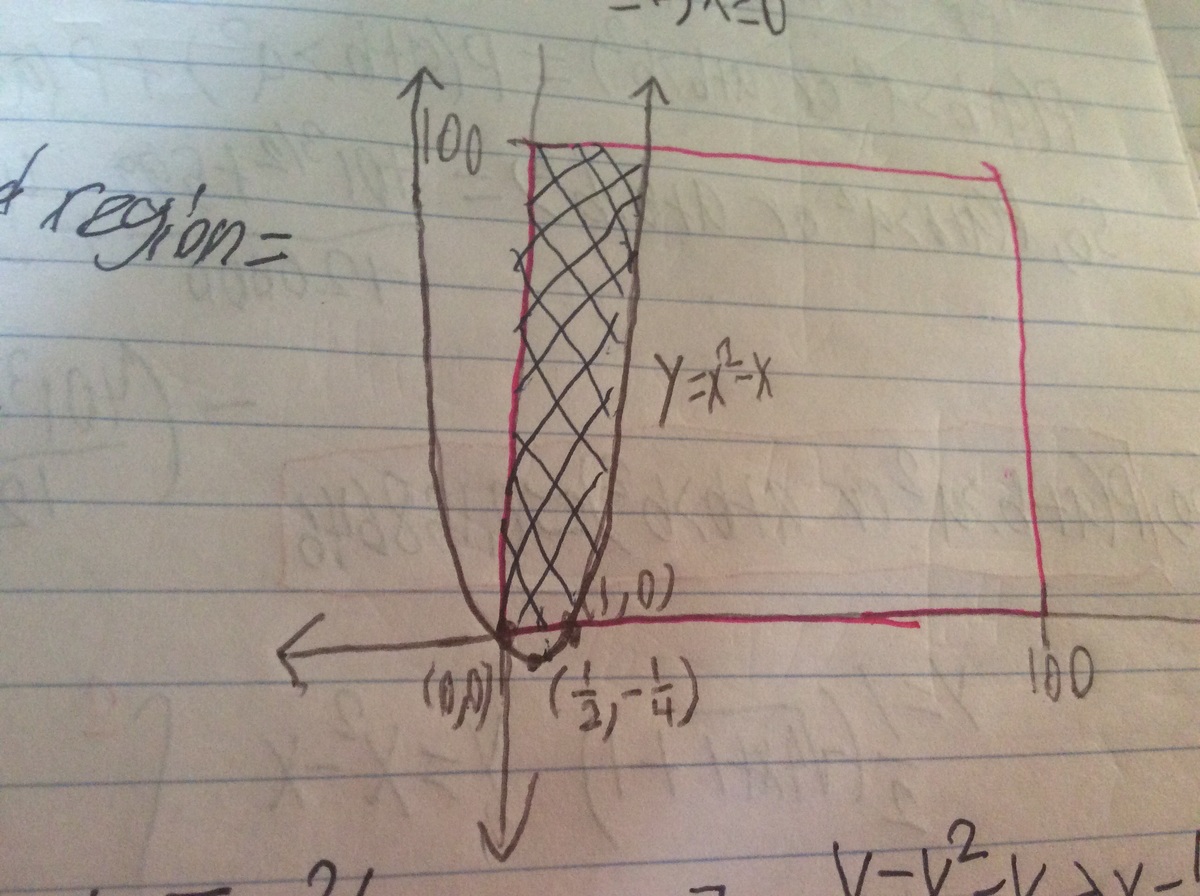
We need to find the area of the shaded part, so we need to integrate y= xΒ²-x along the y-axis from y=0 to y=100. But, we need a function of y to integrate along the y-axis, not x, so we need to solve for x in the equation y= xΒ²-x.

Use the quadratic formula: y=xΒ²-x β‡’ xΒ²-x-y=0 β‡’ x=Β½(1+√(4y+1)) or x= Β½(1-√(4y+1))

If we graph the two functions, we would see that the graph of x= Β½(1-√(4y+1)) does not cross the square(0≀x,y≀100), but x=Β½(1+√(4y+1)) does. So we will be integrating that function across the y-axis to find the β€œgood” area:

∫ β‚€ ¹⁰⁰ Β½(1+√(4y+1)) dy = Β½[(4y+1) Β³/Β²βˆ•6 +y] β‚€ ¹⁰⁰ = Β½([401 Β³/Β²+599]βˆ•6] = [401 Β³/Β²+599]βˆ•12

So, P(x+y>xΒ²)= [401 Β³/Β²+599]βˆ•12 divided by the area of the entire square, which is 100Γ—100=10000. So, P(x+y>xΒ²)= [401 Β³/Β²+599]βˆ•120000. Plug it into the probability equation:

P(x+y>xΒ² or x+y>yΒ²) = 2P(x+y>xΒ²) - P(x+y>xΒ²)Β² P(x+y>xΒ² or x+y>yΒ²)= 2Β·([401 Β³/Β²+599]βˆ•120000) - ([401 Β³/Β²+599]βˆ•120000)Β²

Answerβ‡’ P(x+y>xΒ² or x+y>yΒ²) β‰ˆ 0.138646 β‰ˆ 0.139

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Thanks for posting your write-up. By the way, the link to the diagram doesn't work; but you can insert an image into your solution using the buttons above the editing pane.

The reason we got different answers is a small mistake in your probability calculation. To work out the "or" probability, you need the following:

P ( x + y > x 2 or x + y > y 2 ) = P ( x + y > x 2 ) + P ( x + y > y 2 ) βˆ’ P ( x + y > x 2 and x + y > y 2 ) P\left(x+y>x^2 \text{or } x+y>y^2 \right) = P\left(x+y>x^2\right)+P\left(x+y>y^2\right)-P\left(x+y>x^2 \text{and } x+y>y^2 \right)

But P ( x + y > x 2 and x + y > y 2 ) P\left(x+y>x^2 \text{and } x+y>y^2 \right) is NOT the same as P ( x + y > x 2 ) P ( x + y > y 2 ) P\left(x+y>x^2\right) P\left(x+y>y^2\right)

The easiest way to see this is in the diagram; the region where both x + y > x 2 x+y>x^2 and x + y > y 2 x+y>y^2 is the arrowhead-shaped area enclosed by both near the origin. The two curves cross at x = y = 2 x=y=2 .

The line y = x y=x bisects this region; so to find its area we can find the area between one of the curves and the line y = x y=x and double it.

Using your integration, we want P ( x + y > x 2 and x + y > y 2 ) = 2 10000 ∫ 0 2 1 2 ( 1 + 4 x + 1 ) βˆ’ x d x = 2 10000 [ 1 2 ( x βˆ’ x 2 + 1 6 ( 1 + 4 x ) 3 2 ) ] 0 2 = 7 30000 \begin{aligned} P\left(x+y>x^2 \text{and } x+y>y^2 \right) &= \frac{2}{10000}\int_0^2 \frac12 (1+\sqrt{4x+1}) - x dx \\ &= \frac{2}{10000}\left[ \frac12 \left(x - x^2 + \frac16 (1 + 4 x)^\frac32 \right) \right]_0^2 \\ &=\frac{7}{30000} \end{aligned}

The rest of your calculations are right - it's just that the final result should be P ( x + y > x 2 or x + y > y 2 ) = 2 40 1 3 2 + 599 120000 βˆ’ 7 30000 = 40 1 3 2 + 585 60000 P\left(x+y>x^2 \text{or} x+y>y^2 \right)=2\frac{401^{\frac32} + 599}{120000} - \frac{7}{30000} = \frac{401^{\frac32} + 585}{60000}

Chris Lewis - 10Β months, 2Β weeks ago

0 pending reports

Γ—

Problem Loading...

Note Loading...

Set Loading...