The Summation Sum
n = 1 ∑ 2 0 1 4 [ ( − 1 ) n × ⌊ n ⌋ ] = ?
Notation : ⌊ ⋅ ⌋ denotes the floor function .
The answer is 22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
i under stood this problem easily as follows the sum equals to -1+2-3+4............-43+44 =-1-3-5-7......-43+2+4+6......+44 = -22 * 22 + 23 * 22 = 22 is this true...?
Log in to reply
yeah, but you should be careful about 44
Log in to reply
i exactly did mistake in that 44. thank you
I almost did a mistake because I thought that 44 is leftover from pairing (-1+2)+(-3+4)+...(-43+44)+44.
Yes the whole thing can be simplified into that expression
same to me
this Is exactly what I did
?haha
Between every two perfect squares we have even number of numbers, therefore the greatest integer of the roots of these numbers will be the same e.g - between 4 and 9 all numbers have a greatest integer of 2
so, in the summation, all these numbers cancel out due to the presence of (-1)^n. i.e -1 +( 1 - 1) + 2 +(- 2 + 2 - 2 + 2) -3 .......
hence the remaining values are -1 + 2 - 3 + 4 ...... + 44
Here we can make pairs of two as: (-1 + 2 ) + ( -3 + 4 ) + ..... + ( - 43 + 44 ) which equals to : 1 + 1 + 1 ..... + 1 } 22 times Hence answer = 22
awsome
Why did u take it till 44?
Python
1 2 3 4 5 6 7 8 9 |
|
Hey! I have edited your solution for making it look better. Also, here is a one-liner.
1 2 |
|
Maxima
sum((-1)^n * floor(sqrt(n)), n, 1, 2014), simpsum;
for i in range(2014): k += round(int(math.sqrt(i+0.0)) ((-1) *i)) print k Drat forgot it starts counting from 0. :( Put in -22
I made the same thing, but using C.
Let me see if I can explain purely in English!
1) Each term in the sum is alternating negative and positive, because of the powers of -1. Obviously this starts with a negative term, because -1^1 = -1.
2) Start with 3 terms that are each multiplied by 1, which is the integral part of sqrt 1, sqrt 2 and sqrt 3. Remember that the first of these 3 is negative (since -1^1 = -1). 2 of these terms cancel, leaving one term, which is -1.
3) After n becomes 4, you have 5 terms that are each multiplied by 2, which is the integral part of sqrt 4, sqrt 5, sqrt 6, sqrt 7 and sqrt 8. Remember that the first of these 5 is positive (since -1^4 = 1). 4 of these terms cancel, leaving one term, which is 1 * 2 = 2.
4) Onward like that. In general, after n becomes k^2 (k integer), you have (2k + 1) terms that are each multiplied by k, which is the integral part of sqrt n, sqrt (n+1), ... and sqrt [(k+1) ^ 2 - 1). 2k of these terms cancel, leaving one term that is -k if k is odd, or k if k is even.
5) This pattern continues till n = 1935, and that leaves 79 more terms that are each multiplied by 44 (sqrt 1936).
6) Which leaves us with the series -1 + 2 - 3 + 4 - 5 + 6 ... - 43 + 44.
7) Group those terms 2 at a time, to get 1 + 1 + 1 ... 22 times.
Thus the answer: 22.
This is a nice problem based on the fact that the gaps between any 2 square numbers is always even and so alternate positive and negative values cancels each other.
Now, we are left with odd and even square root of perfect square numbers.
Odd takes negative sign and the series is : -(1+3+5+...+43) = -(22^2) = -484.
Even takes positive sign and the series is : 2(1+2+3+...+22) = 2(22(23)/2) = 506.
Total = 506 - 484 = 22.
After 4 4 2 = 1 9 3 6 , we have 78 numbers in between to reach 2014 which is once again even and cancels each other and hence the answer is 2 2 .
It get break down to following equations. (-1+1-1) +(2-2+2-2+2) + (-3+3-3+3-3+3-3)..............44
-1 + 2 -3 + 4 -5...............+42 - 43 + 44, which can be further split to two simple equations. -1 -3 -5 -7 .... -43 and +2 + 4 +6 .... +44 -484 + 506 = 22
First calculate the sum of the squares. There are 4 4 squares less than 2 0 1 4 . If you rewrite this, it will look like:
− 1 + 2 − 3 + 4 − …
As there's an even quantity of squares ( 4 4 ), we'll get a sum equal to 1 twenty-two times. Thus, the sum of the squares is 2 2 .
Now, for the rest of the numbers, note that between n and n + ( 2 k − 1 ) , where 2 k − 1 is an odd integer (the difference between squares is odd), there are n + ( 2 k − 1 ) − n − 1 = 2 k − 2 possibilities for the radicand, which proofs that there's an even number of possibilities for that. This means that we'll get the same integral value (due to the floor function) in this format:
− + − + … − +
or
+ − + − … + −
Which means that they will cancel (will give 0 ). Also observe that 1 9 3 6 is the highest perfect square less than 2 0 1 4 . So what about 1 9 3 7 , 1 9 3 8 , … , 2 0 1 3 , 2 0 1 4 ? From 1 9 3 7 to 2 0 1 4 there are 2 0 1 4 − 1 9 3 7 + 1 = 7 8 possibilities for the radicand. That's even too, so the same thing will happen, will give us 0 . So we're left just with the sum of the perfect squares, which we've previously evaluated and got the answer:
2 2 .
Input in WolframAlpha:
Sum (-1)^n (Floor [sqrt(n)]), n=1 to 2014
Result = 22
The C code for solution and varying "n" :
#include<stdio.h> #include<conio.h> #include<math.h> int main(){ long long int b,c,d,n,sum; float x; sum=0; for(n=1;n<=2014;n++){ x=pow(n,0.5); b=floor(x); c=pow(-1,n); d=b*c; sum+=d; } printf("the sum is : \%d", sum); getch(); }
Just to add a simple observation that allow you to compute the last part without complicated formula (-1+2)+(-3+4)+... (-43+44) = 1+1... +1 = 22
Please correct integral into integer.
We have powers of 1 followed by lower integer function. Starting the series would reveal it as : -1, 1, -1, 2, -2, 2, -2, 2,....... Let's go till 1935 terms which is -43. Now 1936th term is 44 and 2014th term is also 44. Now adding all terms we get something like -1+2-3+4-5..........-43+44. Now taking two terms at a time we get 1+1+1+......... 22 times. So answer is 22. Ola!!!!
(-1)^(n)X[sqrt(n)]+(-1)^(n-1)X[sqrt(n-1)]=1, if sqrt(n)=[sqrt(n)] and n%2=0 (-1)^(n)X[sqrt(n)]+(-1)^(n+1)X[sqrt(n+1)]=0, if sqrt(n)=[sqrt(n)] and n%2=1 otherwise: (-1)^(n)X[sqrt(n)]+(-1)^(n-1)X[sqrt(n-1)]=0 sqrt(2014)=44 result = (2^{2}-3)+(4^{2}-15)+...+(44^{2}-(44^{2}-1))=22
The term will be as follows -1+1-1+2 upto 4terms.. and if u observe a pattern, u will find a net value of +1 for every consecutive perfect squares. As the Sq.root of 1936 is 44. So for a value of 'n' upto 1936. The net sum is 22. and the sum of values from 1937 to 2014 is zero. (As the next perfect square is at 2025.). Hence the net value is 22.
Answer = -1+2-3+4-5+6-.......-44 On simplifications it yields to give '22' Therfore Correct answer = 22
Expand the summation and after some amount of heuristics you will find that the integral part after taking the root will be all natural numbers from 1 to 44 since 2014 is less than the square of 45. So finally the series is going to be as follows- -1 + 2 - 3 + 4 - 5 + 6 - 7 + . . . - 43 + 44 whose summation is equal to 22.
its jst the sum like that -1+2-3+4-5........upto 44
let s be the sum, before 4(2^2),s=-1 before 9(3^2),s=-1+2 similarly before 1936(44^2) sum will be -1+2-3+4-5+6.........-43, therefore finalsum=-1+2-3+4-5+6......+44=22
I think my solution was the same......... : - ) GOOD JOB!
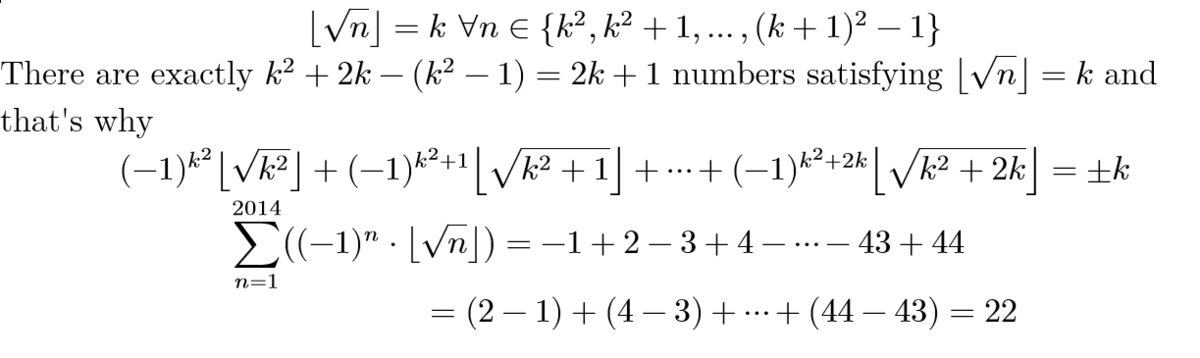
To get a feel for this sum, first write out a few terms: − 1 + 1 − 1 + 2 − 2 + 2 − 2 + 2 − 3 + ⋯
Each ⌊ n ⌋ term is the square root of the largest square before n . From the difference of squares factorization, ( n + 1 ) 2 − ( n ) 2 = ( n + 1 − n ) ( n + 1 + n ) = 2 n + 1 , so there are 2 n + 1 terms that are equal to n ; this is always an odd number.
Now note that, for any sum ∑ k = 1 2 n + 1 ( − 1 ) k ⋅ n , all the terms cancel each other except the first term. For n = 1 , the first term is negative, and for n = 4 it is positive. Because there are an odd number of terms between the n s, the parity of the leading terms will repeat, and from these initial cases inductively it is that the odd n s have negative leading terms and the even n s have positive leading terms.
Now consider the sum ∑ n = 1 1 9 3 5 ( − 1 ) n ⋅ ⌊ n ⌋ . Because of the canceling mentioned above, this is merely ∑ k = 1 4 3 ( − 1 ) k ⋅ k , which can be grouped to form ( 2 2 ) ( − 1 ) = − 2 2 .
Now we must finally consider the sum ∑ n = 1 9 3 6 2 0 1 4 ( − 1 ) n ⋅ ⌊ n ⌋ = ∑ n = 1 9 3 6 2 0 1 4 ( − 1 ) n ⋅ 4 4 . Because 4 4 is even, the leading term will be positive, and because there are an odd number of terms they will cancel except the first one. Thus this sum is equal to 4 4 .
So, to finish, n = 1 ∑ 2 0 1 4 ( − 1 ) n ⋅ ⌊ n ⌋ = n = 1 ∑ 1 9 3 5 ( − 1 ) n ⋅ ⌊ n ⌋ + n = 1 9 3 6 ∑ 2 0 1 4 ( − 1 ) n ⋅ ⌊ n ⌋ = ( − 2 2 ) + ( 4 4 ) = 2 2