The Sunrise
During a sunrise, it is possible to see the sun even if it is below the horizon. This caused by a refraction effect, also called atmospheric refraction : the atmosphere acts on the light coming from the sun as a glass of water.
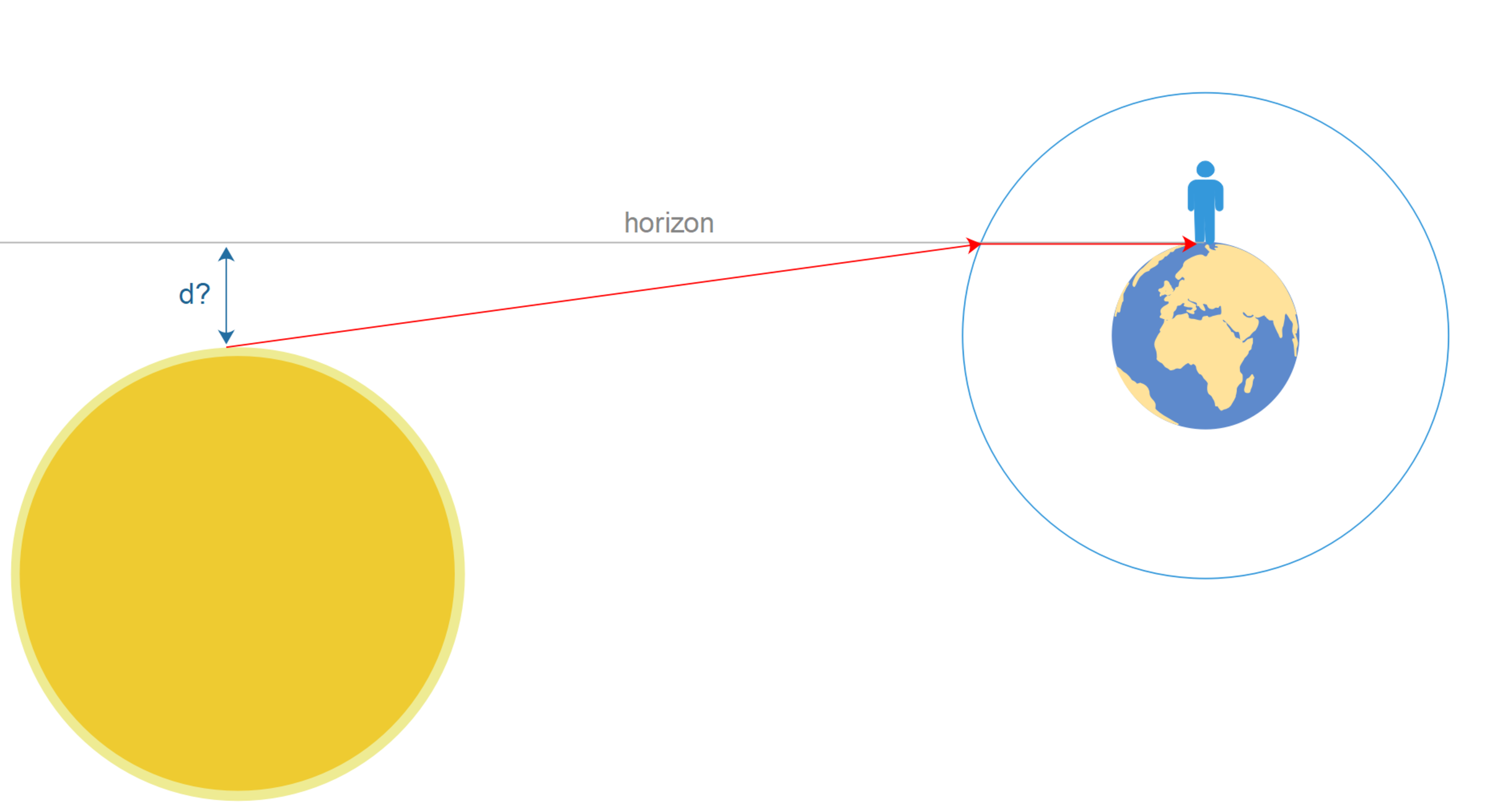
What is the distance of the sun under the horizon at the beginning of the sunrise?
Assumptions and Hints:
1) Model the atmosphere as sphere over the earth containing air with a refraction index n = 1 . 0 0 0 3 . The height of the atmosphere over the earth's surface, can be considered to be around 1 2 km .
2) The distance between the earth and the sun is D E S = 1 5 0 million km and the earth's radius is 6 3 7 0 km .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
lol flat Earthers will believe the Earth is flat because of this xD
Let the angle of incidence be α and the angle of refraction be β . Then sin β = R + h R ≈ 0 . 9 9 8 1 9 9 ⟹ cos β ≈ 0 . 0 6 1 2 9 , cot β ≈ 0 . 0 6 1 4 . Here R and h are the radius of earth and height of atmosphere respectively. Also sin ( α − β ) ≈ α − β ≈ S d = 1 5 0 × 1 0 6 d . R.I. of atmosphere = n = 1 . 0 0 0 3 = sin β sin α ≈ 1 + ( α − β ) cot β ⟹ α − β = cot β 0 . 0 0 0 3 ≈ 0 . 0 0 4 8 8 . So 1 5 0 × 1 0 6 d ≈ 0 . 0 0 4 8 8 ⟹ d ≈ 7 3 2 8 3 5 . 8 2 km.
Let's consider an atmosphere with radius R E + h and a single refraction coefficient n A . In reality, the coefficient depends on the height of the atmosphere, so we should integrate the influence of it over the height (this would complicate the problem a lot).
We can use Snell's Law (https://brilliant.org/wiki/snells-law/) to relate the angle of incidence θ 1 = θ 2 + Δ θ and the angle of refraction θ 2 :
n v o i d sin θ 1 = n A sin θ 2
( n v o i d = 1 )
Using some geometry, we can determine the sine of the angle of refraction: sin θ 2 = R E + h R E . The expression simplifies to:
θ 1 = sin − 1 [ n A R E + h R E ]
...so the angle Δ θ = sin − 1 [ n A R E + h R E ] − sin − 1 [ R E + h R E ]
With this angle, we can now determine the distance of the sun under the horizon d :
d ≈ ( D E S − h ) ⋅ Δ θ ≈ D E S ⋅ Δ θ .
So: d ≈ D E S ⋅ ( sin − 1 [ n A R E + h R E ] − sin − 1 [ R E + h R E ] ) = 7 5 0 0 0 0 km