The Tale of 2 Chords
Geometry
Level
1
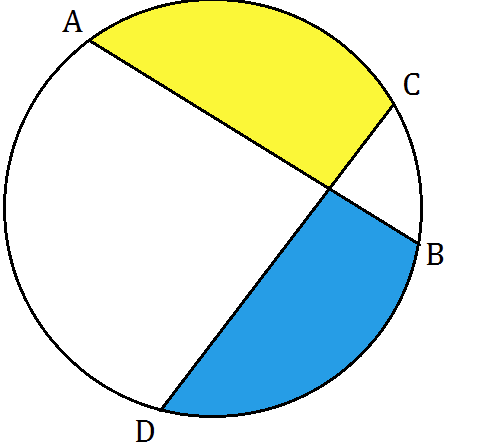
As shown, a circle has 2 chords AB = CD.
Are the yellow and blue areas always equal?
No, not necessarily.
Yes, always!
No, never!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let O be the center of the circle and E the intersection point of both chords.
If AB = CD, then the triangle OAB is congruent to OCD because of equal 3 sides; they are also isosceles triangles.
That makes the angle OAD = angle ODA = x and angle OCD = angle ODC = angle OBA = angle OAB = y, according to isosceles property.
Thus, arithmetically, the angle DCB = angle BAD = x+y, making the triangle AED also an isosceles triangle. That means AE = ED and EC = EB because AB = CD.
That makes the triangle AEC congruent to BED because angle AEC = angle BED, so AC = BD and the arc AC = arc BD.
As a result, the both colored portions are congruent because of all equal side lengths and will have the same area.
Note: The quadrilateral ABCD is an isosceles trapezoid because angle ABC = angle CDA due to angle of the same arc. Thus, AD // BC and AC = BD.