The tangency point

Geometry Level 5

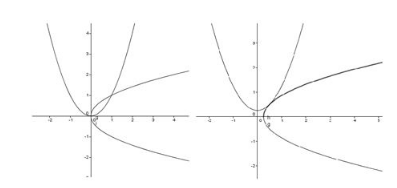
Let there be 2 graphs of 2 parabolas, $(1): y = x^2$ , $(2): x=y^2$ as shown in the figure.

The graph of the parabola $(1)$ moves along the $y$ -axis from the bottom to the top as the parabola $(2)$ shifts to the right.

What is the sum of coordinates of the tangency of the point?

The answer is 1.

1 solution

Chew-Seong Cheong
Dec 24, 2016

The answer should be $\boxed{1}$ .

The shifted parabolas are:

$\begin{cases} (1a): & y_1 = x^2 + \frac 14 \\ (2a): & x-\frac 14 = y_2^2 \end{cases}$

And the point of tangency is $\left(\frac 12, \frac 12\right) \implies \frac 12 + \frac 12 = \boxed{1}$

Let us check if $y_1=y_2 = \frac 12$ and $\dfrac {dy_1}{dx} = \dfrac {dy_2}{dx}$ , when $x=\frac 12$ .

$\begin{cases} y_1 = \left(\frac 12\right)^2 + \frac 14 & \implies y_1 = \frac 12 \\ \frac 12 -\frac 14 = y_2^2 & \implies y_2 = \frac 12 \end{cases}$

$\begin{cases} \dfrac {dy_1}{dx} = 2x & \implies \dfrac {dy_1}{dx}\bigg|_{x=\frac 12} = 1 \\ 1 = 2y_2 \dfrac {dy_2}{dx} & \implies \dfrac {dy_2}{dx}\bigg|_{x=\frac 12} = 1 \end{cases}$

@Chew-Seong Cheong , we really liked your comment, and have converted it into a solution. If you subscribe to this solution, you will receive notifications about future comments.

Brilliant Mathematics Staff - 4 years, 5 months ago

The tangency point

The answer is 1.

1 solution

0 pending reports