The tank is leaking
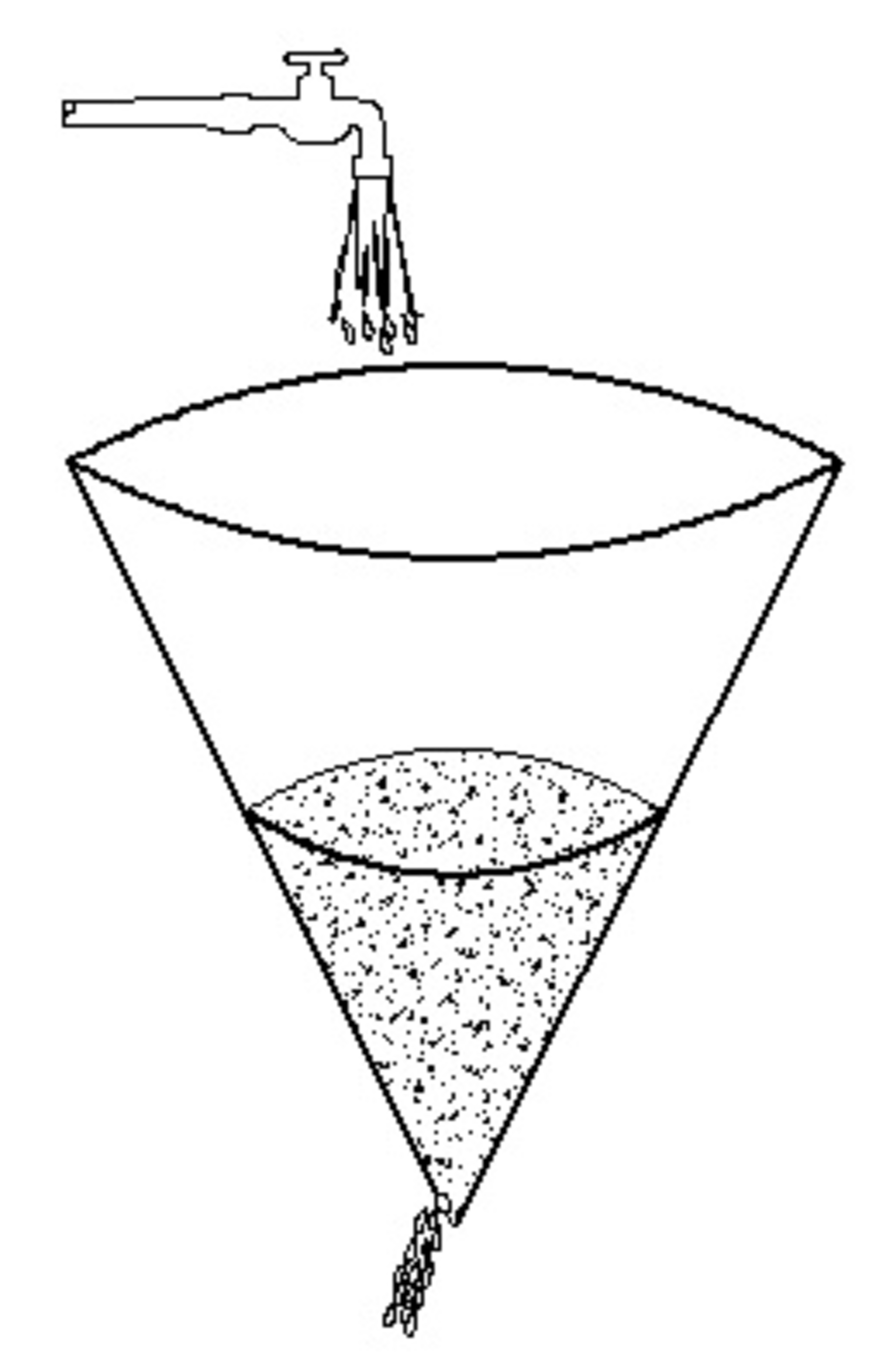 Water at the rate of
is pouring into a tank whose shape is right circular cone
deep and
diameter at the top. At the time the water is
deep, the water level is observed to be rising
.
If the tank has a leak at the bottom, how fast is the water leaking in
?
Water at the rate of
is pouring into a tank whose shape is right circular cone
deep and
diameter at the top. At the time the water is
deep, the water level is observed to be rising
.
If the tank has a leak at the bottom, how fast is the water leaking in
?
Use .
The answer is 0.58.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Related Rates of Change - Basic
By ratio and proportion,
4 x = 1 6 y
x = 1 6 4 y = 4 y
The volume of water at anytime is
V = 3 1 π x 2 y
However, x = 4 y
Substituting, we obtain
V = 3 1 π ( 4 y ) 2 y
V = 3 1 π ( 1 6 y 3 )
V = 4 8 1 π y 3
Differentiate both sides with respect to t .
d t d V = 4 8 1 π ( 3 ) ( y 2 ) ( d t d y )
d t d V = 1 6 1 y 2 d t d y
However, when y = 1 2 c m , d t d y = 3 1 m i n c m
Substituting, we obtain
d t d V = 1 6 1 π ( 1 2 2 ) ( 3 1 )
d t d V = 3 π = 3 ( 3 . 1 4 ) = 9 . 4 2 m i n c m 3
Finally, the water at the bottom of the tank is leaking at the rate of 1 0 − 9 . 4 2 = 0 . 5 8 m i n c m 3