The Three Circles
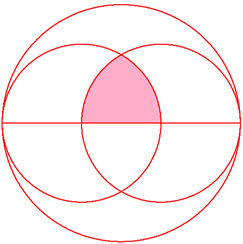 In the above diagram, we have one big circle and two small circles of equal size. The straight line is the diameter of the big circle. The distance between the centers of the small circles is 1/3 the length of the diameter of the big circle.
In the above diagram, we have one big circle and two small circles of equal size. The straight line is the diameter of the big circle. The distance between the centers of the small circles is 1/3 the length of the diameter of the big circle.
To two decimal places, what percentage is the shaded area out of the area of the big circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nicely done, Sean. Well explained and much better looking than my solution. :)
Got wrong answer as calcultaed the two areas.Nice options.
Why the area of the big circle is 9.pi.r((sqr)2)/4? not 9.pi.r((sqr)2)? . I can't imagine which area is pi.r((sqr)2)/3 and where is the position of equilateral triangle. Would you explain it by picture? sorry for my bad english, you are my only option.
nice solutionsean
Very well done. I used Calculus to get the answer and it was considerably more complex.
why the area is pi r2/6 for big ....and /3 for small ....i didnt under stand this step
Good, almost the same than me
Since the centers of the smaller circles are separated by a distance 1/3 the diameter of the big circle, the radii of the smaller circles are also 1/3 the diameter of the big circle. This also means that each of the smaller circles passes through the center of the other smaller circle. This means that the area of the shaded region is that of 2 sectors of the smaller circles subtended by angles of pi/3 radians, minus the area of the equilateral triangle they share in common that is formed by their centers and the upper point of intersection. If the radius of the smaller circles is R, then the area of the shaded region is
2 * (1/6) * pi * R^2 - (1/2) * R * (1/2) * sqrt(3 )* R =
[(pi/3) - (1/4) * sqrt(3)] * R^2.
Now the area of the big circle will be pi [(3/2) R]^2 = (9/4) pi R^2, giving us a fractional area of [(pi/3) - (1/4) sqrt(3)] / [(9/4) pi] = 0.0869 to 3 significant figures, or 8.69%.
Sorry about the formatting. I really need to learn LaTex. :)
Log in to reply
you can learn the commands on http://www.artofproblemsolving.com/Wiki/index.php/LaTeX:Commands
Log in to reply
Thanks for the link, Shriram. I look forward to learning the commands. )
I got so frustrated putting in answers like . 0 8 6 8 8 , . 0 9 , and . 0 8 7 , but when I finally saw the answer and saw 'percentage' I nearly tore my hair out.
Log in to reply
I put in 8.6889% cause I did not see where it specified to round. I feel ya'.
I'll try my best to improve it later. For now, time for school.
Let the radii of the smaller circles be 2 r and the bigger circle be 3 r . The shaded area is formed by 2 overlapping sectors 6 0 ∘ each. Their area is 6 π r 2 each, and 3 π r 2 for both.
But we counted a region twice. An equilateral triangle to be exact. So we draw the equilateral triangle inside the shaded region. The area of the triangle is 4 r 2 3 .
Subtracting the area of the triangle from the area of the two sectors gives us the area which is r 2 ( 3 π − 4 3 )
The area of the biggest circle is 4 9 π r 2 .
Dividing the two areas and multiplying by 100, we get 8.6889 or approximately
8 . 6 9