The three-digit number with a twist
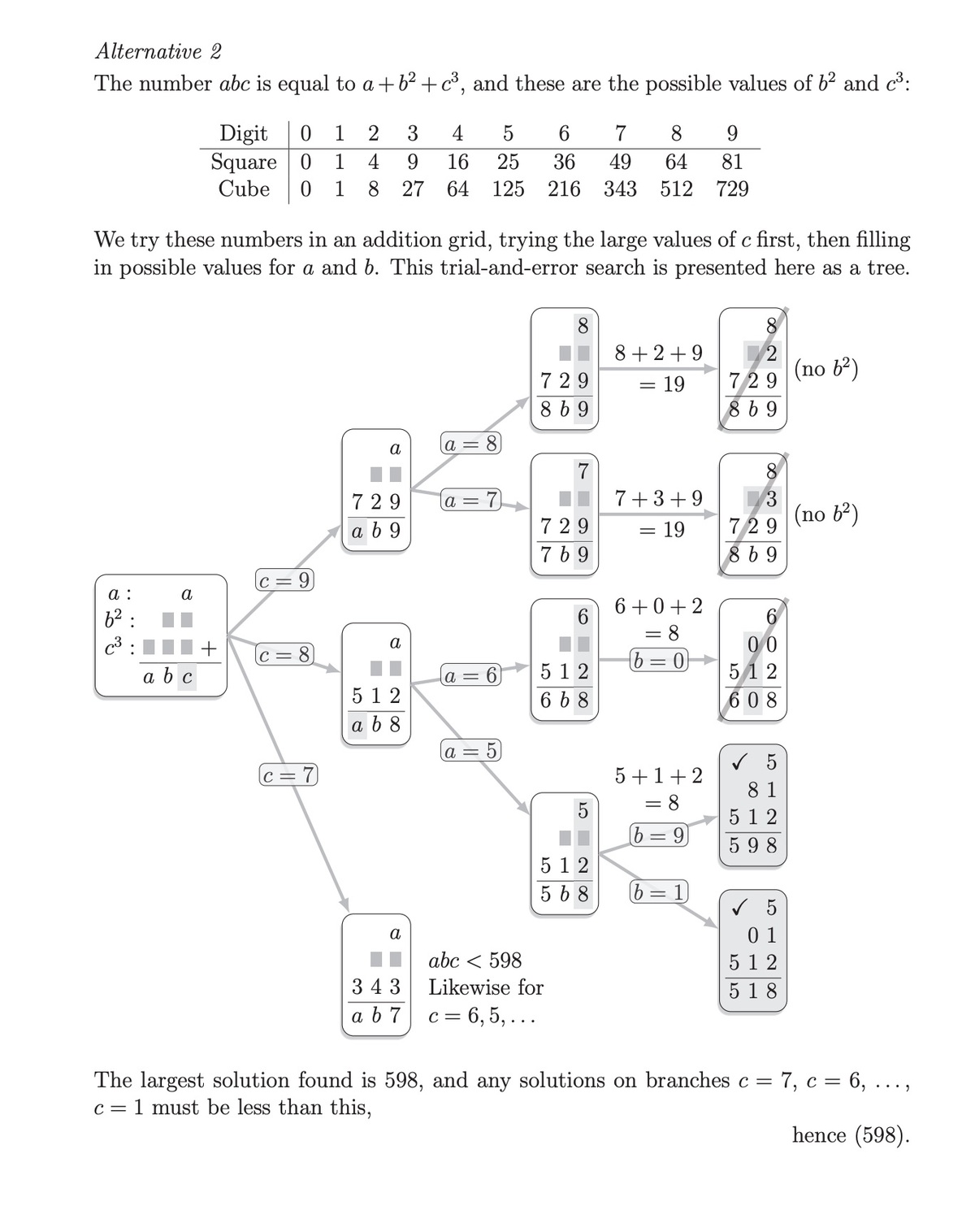
What is the largest three-digit number with the property that the number is equal to the sum of its hundreds digit, the square of its tens digit and the cube of its units digit?
The answer is 598.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions

Interesting...
Let the three-digit number be a b c :
1 0 0 a + 1 0 b + c = a + b 2 + c 3
By rearranging, we get:
9 9 a + b ( 1 0 − b ) = ( c − 1 ) c ( c + 1 )
Seeing that when a = b = 4 , 7 and c = 3 , 8 , it produces solutions, substitute these values into the equation. We get:
n = 1 3 5 , 1 7 5 , 5 1 8 , 5 9 8 .
Therefore n = 5 9 8 is the largest solution.
1 2 3 4 5 6 7 |
|
Output
1 2 3 4 |
|
The largest number is 5 9 8