The three wedges of Po
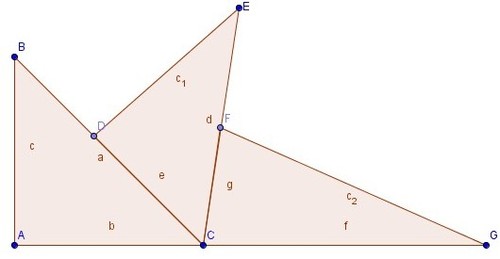In the figure above, there are three perpendicular wedges as shown where
∠
A
=
∠
D
=
∠
F
=
9
0
°
.
Further
A
C
=
D
C
=
F
C
=
P
and
A
B
=
x
,
D
E
=
y
,
F
G
=
z
.
The points A, C & G are collinear. Find the value of
P
2
(
x
y
1
+
y
z
1
+
z
x
1
)
.
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Have done exactly that!!
I prove (why) for you: θ 1 + θ 2 + θ 3 = π , so that θ 1 + θ 2 = π − θ 3 , so that tan ( θ 1 + θ 2 ) = − tan θ 3 then 1 − tan θ 1 tan θ 2 tan θ 1 + tan θ 2 = − tan θ 3 then tan θ 1 + tan θ 2 + tan θ 3 = tan θ 1 tan θ 2 tan θ 3
You might want to amend the problem to explicitly state that A, C, G are collinear. It sure looks like they are, and your solution assumes this hypothesis, but it is best to spell out these things so everyone knows what you are thinking. Nice problem!
What do you mean by placing (why) in parenthesis? Is this a question you asking other readers or yourself? The last two lines are unclear. I solved the problem by using te formula for tangent of the sum of angles. A few more lines with some algebraic manipulations but it worked just fine.
Log in to reply
You may consider it as an exercise in itself. I use it whenever i use direct results.
I took a geometric approach. Angle ACB + Angle DCE + Angle FCG = 180 degrees, since they form a straight line. Now, let AC = DC = FC = P = 1. Let angles ACB, DCE, and FCG all be 60 degrees. Then angles ABC, DEC, and FGC are all 30 degrees. In a 30-60-90 right triangle with side 1, the other non-hypotenuse side is square root of 3. Therefore, we have P^2(1/xy + 1/yz + 1/zx) = 1(1/3 + 1/3 + 1/3) = 1(1) = 1.
That is not a geometric approach. I would possibly call that a heuristic approach. You reasoned that if there were a unique solution regardless of the angles, that making them all 60 ought to work as well. Not rigorous, but in a pinch this can be used as long as you KNOW that there can be only one answer.
Assume P=x=y, then z is infinite, then the answer is simply 1.
Let ∠ A C B = θ 1 , ∠ D C E = θ 2 , ∠ F C G = θ 3 . Now tan θ 1 = P x , tan θ 2 = P y , tan θ 3 = P z ⇒ θ 1 = tan − 1 ( P x ) , θ 2 = tan − 1 ( P y ) , θ 3 = tan − 1 ( P z ) Now θ 1 + θ 2 + θ 3 = tan − 1 ( P x ) + tan − 1 ( P y ) + tan − 1 ( P z ) = π ⇒ ( P x ) ( P y ) ( P z ) = ( P x ) + ( P y ) + ( P z ) ( w h y ) ⇒ P 2 ( x y 1 + y z 1 + z x 1 ) = 1