The time before they met - 2
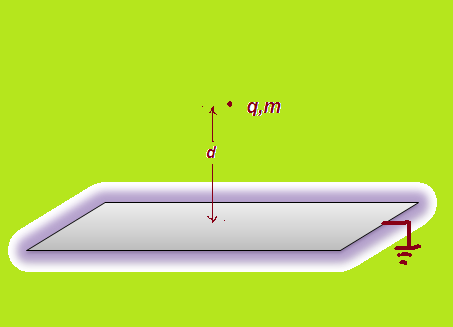 Determine the time for the charge q (mass m) touch the conducting plane as shown above
if the time is
find
Determine the time for the charge q (mass m) touch the conducting plane as shown above
if the time is
find
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Denote the conducting plane to be the x-y plane, and orthogonal to it the z-axis, in which the actual charge lies on, i.e. its position co-ordinates are (0, 0, d). By the first uniqueness theorem, we can replace the grounded plate with an image point charge of -q a distance 2d away from the actual charge of +q as it allows for the potential along the x-y plane to remain zero. Simply put, the image charge has charge -q and co-ordinates (0, 0, -d).
The only (non-negligible) force of interaction is that of the Coloumbic attraction between the 2 charges or magnitude 4 π ε 0 1 ( 2 d ) 2 q 2 , making this essentially a central force problem. Thus, we denote the reduced mass as μ = m 1 + m 1 1 = 2 m . That being said, we can now visualise the problem as some random body of mass 2 m crashing into some place 2d away under the influence of some pre-existing force.
By energy conservation, we obtain 2 μ ( d t d r ) 2 − 4 π ε 0 1 r q 2 = − 4 π ε 0 1 2 d q 2 . Rearranging and solving the differential equation via integration by substitution, we obtain x=3/2 and y=2, giving the answer as 5.