The time now is 7:00.
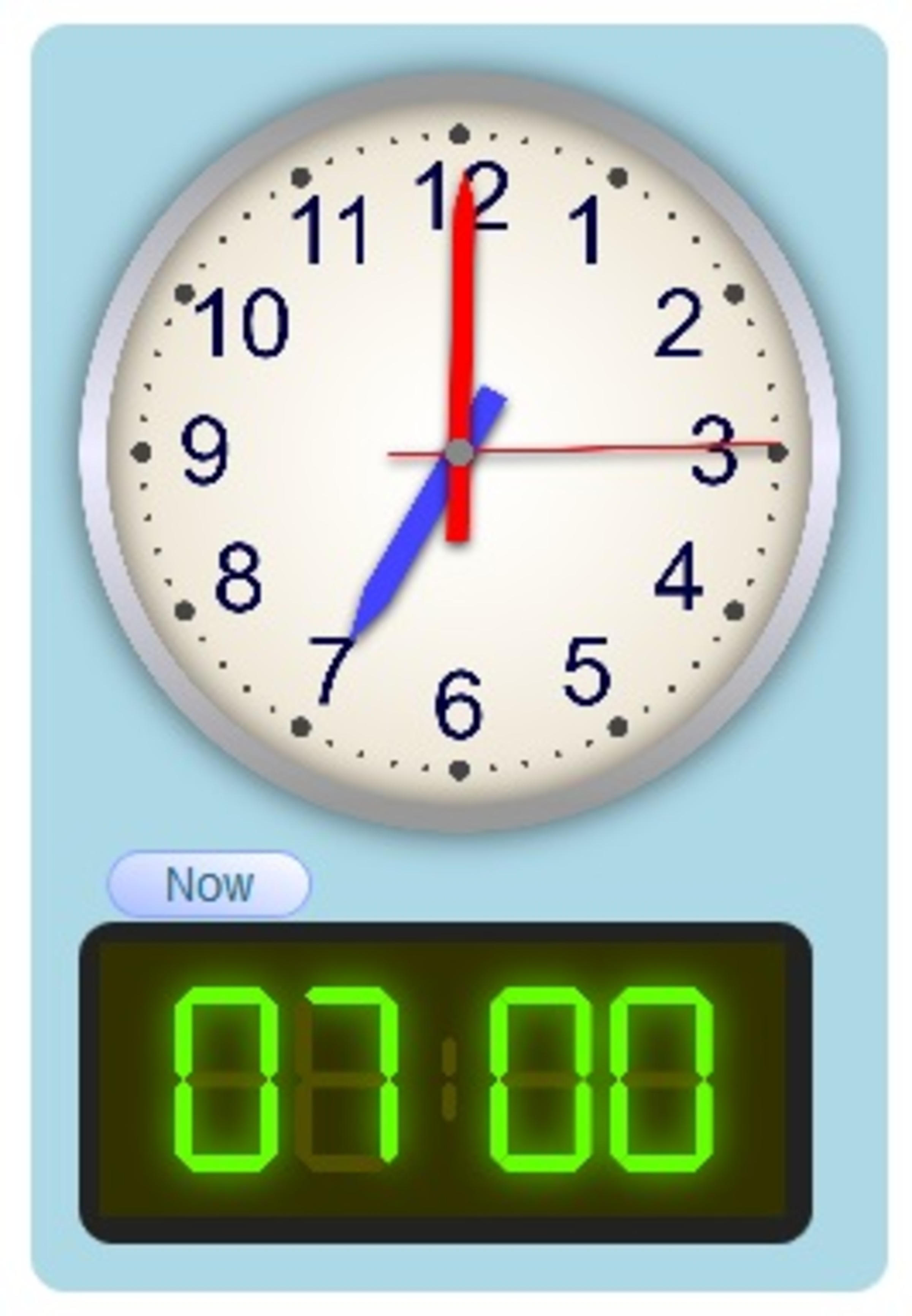 At what time after
7
:
0
0
will the minute hand overtake the hour hand?
At what time after
7
:
0
0
will the minute hand overtake the hour hand?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let
ω
h
and
ω
m
be the angular frequency of the hour hand and the minute hand respectively.
The hour hand completes one full revolution (
2
π
rad) every 12h=12*60m. So:
ω
h
=
1
2
∗
6
0
2
π
=
3
6
0
π
m
r
a
d
The minute hand complete one full revolution (
2
π
rad) every 60m. So:
ω
m
=
6
0
2
π
=
3
0
π
m
r
a
d
Now, we let
θ
h
be the angle (counting clockwise) between the vertical position and the hour hand and
θ
m
the angle between the vertical position and the minute hand. If we consider
t
=
0
the moment at which the clock shows 7:00 o'clock then the starting angles are:
θ
h
(
0
)
=
1
2
7
2
π
=
6
7
π
r
a
d
and
θ
m
(
0
)
=
0
r
a
d
. Therefore we have:
θ
h
(
t
)
=
θ
h
(
0
)
+
ω
h
∗
t
=
6
7
π
+
3
6
0
π
t
θ
m
(
t
)
=
θ
m
(
0
)
+
ω
m
∗
t
=
3
0
π
t
We want to find the moment at which the two hands are on top of one another. That is the moment at which
θ
m
=
θ
h
. So:
3
0
π
t
=
6
7
π
+
3
6
0
π
t
Working out some tedious algebra we conclude that:
t
=
1
1
7
∗
6
0
=
3
8
+
1
1
2
m
So the answer is:
7
:
3
8
1
1
2
x = 3 5 + 1 2 x ⟹ x = 3 8 1 1 2
Thus, the minute hand will overtake the hour hand at 7 : 3 8 1 1 2 .