The Total Area ( 1 )

Geometry Level 2

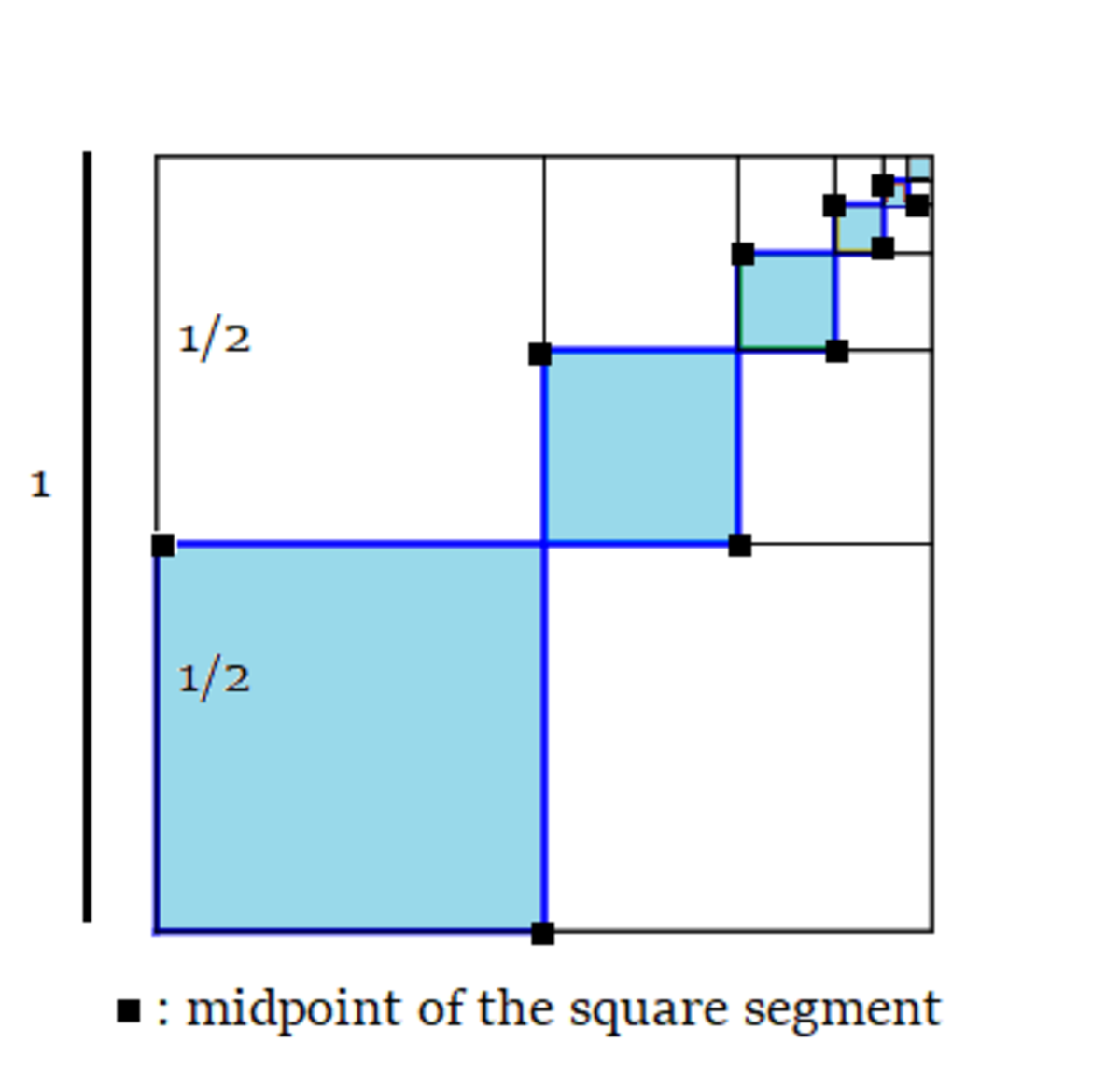
The side of the large square is 1 1 unit and each black point divides its corresponding segment in half. If this blue area continues in this pattern, then what is the total area in blue?

Image credit and problem source : Wolfram

1 8 \frac{1}{8} 1 2 \frac{1}{2} 1 5 \frac{1}{5} 1 3 \frac{1}{3} 1 4 \frac{1}{4}

Hana Wehbi by Hana Wehbi , 51, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Ron Gallagher
May 15, 2020

The area is of the whole square is 1 unit. The area of the first blue square is 1/4 of the total. The area of the next blue square is 1/4 of 1/4 of the total (i.e., (1/4)^2. Continue in this fashion. The total area is then 1/4 + (1/4)^2 + (1/4)^3 + ... = (1/4)*(1/(1-1/4)) = 1/3

2 Helpful 0 Interesting 0 Brilliant 0 Confused
David Vreken
May 15, 2020

This L-shape is infinitely repeated in the diagram:

and since it is 1 1 part blue square to 3 3 total squares, the total area is A = 1 3 ⋅ 1 2 = 1 3 A = \frac{1}{3} \cdot 1^2 = \boxed{\frac{1}{3}} .

1 Helpful 0 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...