The tower
Given the following function (also called infinite exponential tower):
f ( a ) = a a a a a a a a . . .
Where a is a positive real number
Let a 0 be the maximum value of a so that the function has a definite value and f ( a 0 ) = b
What is a 0 + b
Submit your answer as ⌊ 1 0 0 0 0 ( a 0 + b ) ⌋
Note: ⌊ . ⌋ is the floor function
*Note: though it may be possible to solve this problem manually all the way, my solution involves a little bit of programming. If anyone has a solution that is entirely manual, please tell me in the solution section. Thank you. *
The answer is 41629.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let f ( a ) = x . It's easy to see that x = a x
Now we find the maximum value a 0 of a so that the equation x = a x has a real solution x 0
The solution is the intersection of two graphs: y = x and y = a x
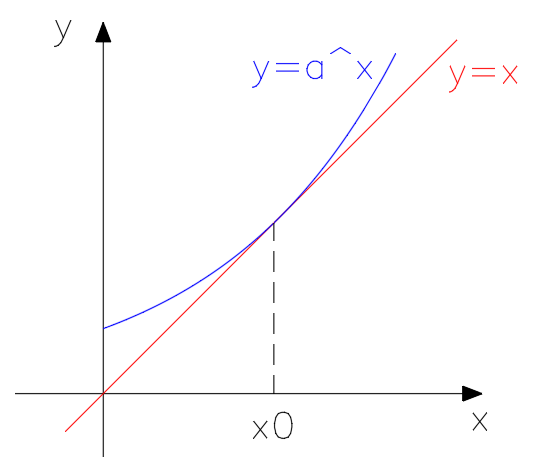
The maximum value of a is when the line y = x is tangent to the curve y = a x
The tangent line equation y = y ′ ( x − x 0 ) + y 0 ≡ y = x where ( x 0 , y 0 ) is the point of intersection
y = a x 0 ln a ( x − x 0 ) + a x 0
We know y ′ ( x 0 ) = 1 and the tangent line goes through ( 0 , 0 ) so:
a x 0 ln a = 1 x 0 − a x 0 = 0
≡ x 0 ln a = 1 x 0 − a x 0 = 0
≡ ln a 1 − a ln a 1 = 0 x 0 − a x 0 = 0
Now we use Newton's method to solve the first equation than substitute it into the second one. This is when programming comes in handy
Newton's method: x n = x n − 1 − f ′ ( x n − 1 ) f ( x n − 1 )
Now copy and paste all of these code lines into python (I'm sorry I don't know how to put a python window here):
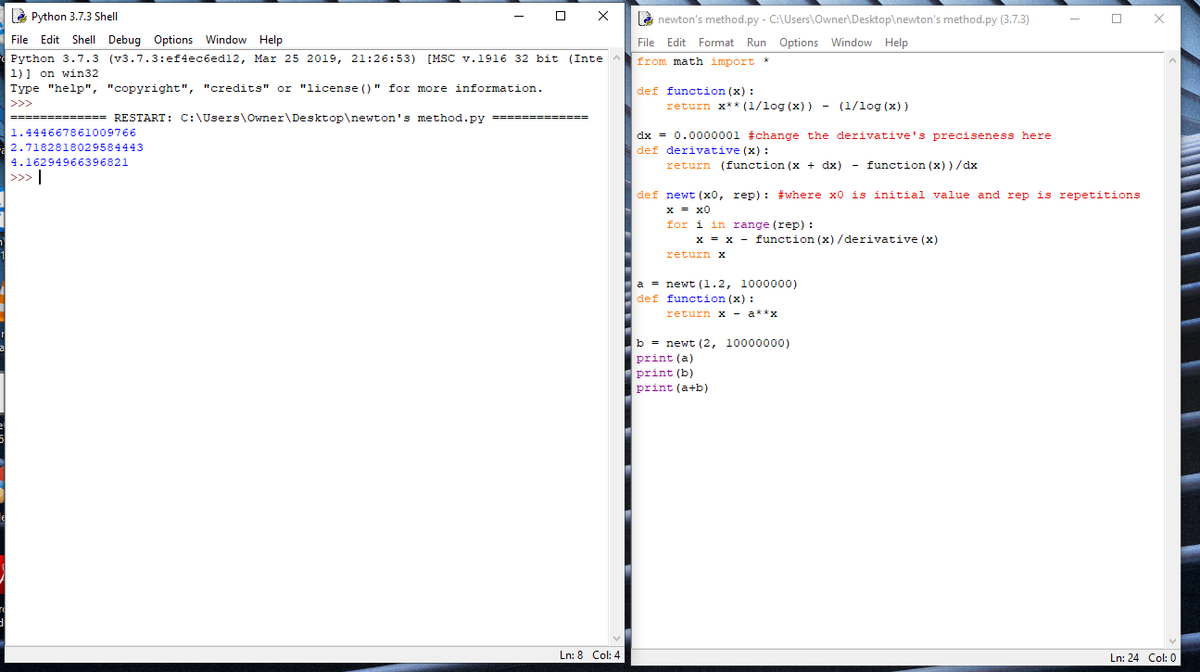
The program gives:
a = 1.444667861
b = 2.718281802
a + b = 4.162949663
The "entirely manual" solution works like yours - once you get to the equation lo g a 1 − a lo g a 1 = 0 , just substitute t = lo g a . The equation becomes t 1 − ( e t ) t 1 = 0 . But this is just t 1 − e = 0 , and so we find a = e e 1 .
As mentioned here , Euler showed that f ( a ) converges only when e e 1 ≤ a ≤ e e
The maximum value of the given expression is b=e, when a=e^(1/e)
I'm not too familiar with latex, so here is a written 'manual solution' :)