The trapezoid is trapped in the circle!
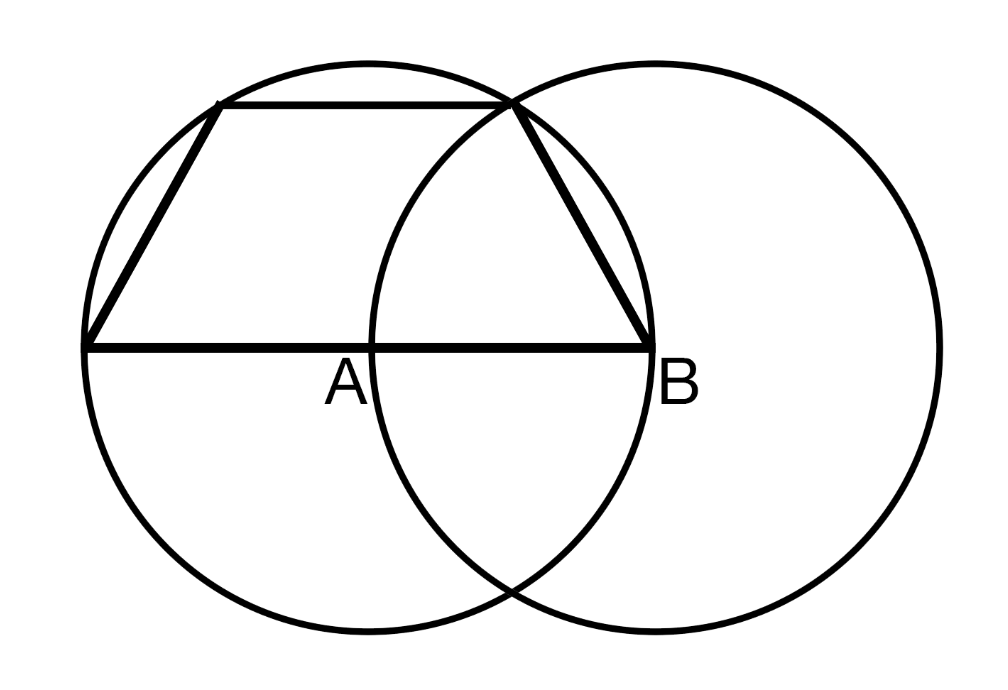
We see circles A and B of radius 1 in the diagram. Find the area of the trapezoid. If this area is expressible in the form c a b , where a , c are coprime and b is square-free, find a + b + c .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
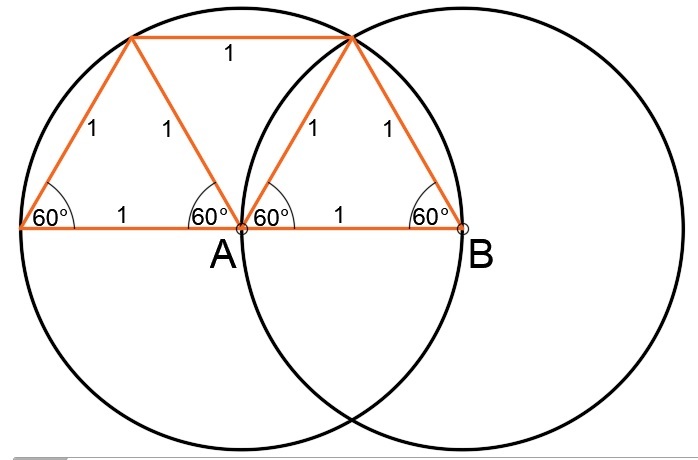 Consider my diagram. The trapezoid is composed of three congruent equilateral triangles. The area of an equilateral triangle is given by
A
=
4
3
x
2
where
x
is the side length. Therefore, the area of the trapezoid is
A
=
3
(
4
3
)
(
1
2
)
=
4
3
3
.
Consider my diagram. The trapezoid is composed of three congruent equilateral triangles. The area of an equilateral triangle is given by
A
=
4
3
x
2
where
x
is the side length. Therefore, the area of the trapezoid is
A
=
3
(
4
3
)
(
1
2
)
=
4
3
3
.
Thus, the desired answer is a + b + c = 3 + 3 + 4 = 1 0
The trapezoid can be split into three congruent equilateral triangles as shown below: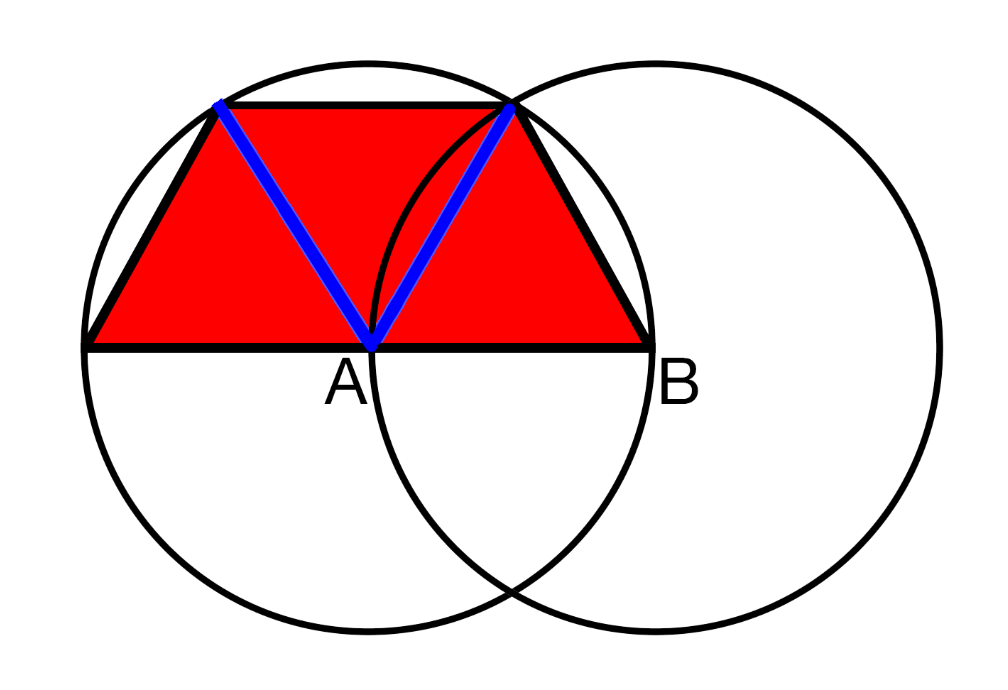 Since the radius, which is the same as the sides as the sides of the equilateral triangles, is
1
, we can use our equilateral triangle area formula to find out the area:
A
=
4
s
2
⋅
3
Our side length is
1
, so therefore we can get rid of the
s
2
in the equation:
A
=
4
3
Since we have three equilateral triangles, remember to multiply by three:
A
=
4
3
3
That’s our area, so
a
+
b
+
c
=
1
0
Since the radius, which is the same as the sides as the sides of the equilateral triangles, is
1
, we can use our equilateral triangle area formula to find out the area:
A
=
4
s
2
⋅
3
Our side length is
1
, so therefore we can get rid of the
s
2
in the equation:
A
=
4
3
Since we have three equilateral triangles, remember to multiply by three:
A
=
4
3
3
That’s our area, so
a
+
b
+
c
=
1
0