The trapped gemstone
Geometry
Level
pending
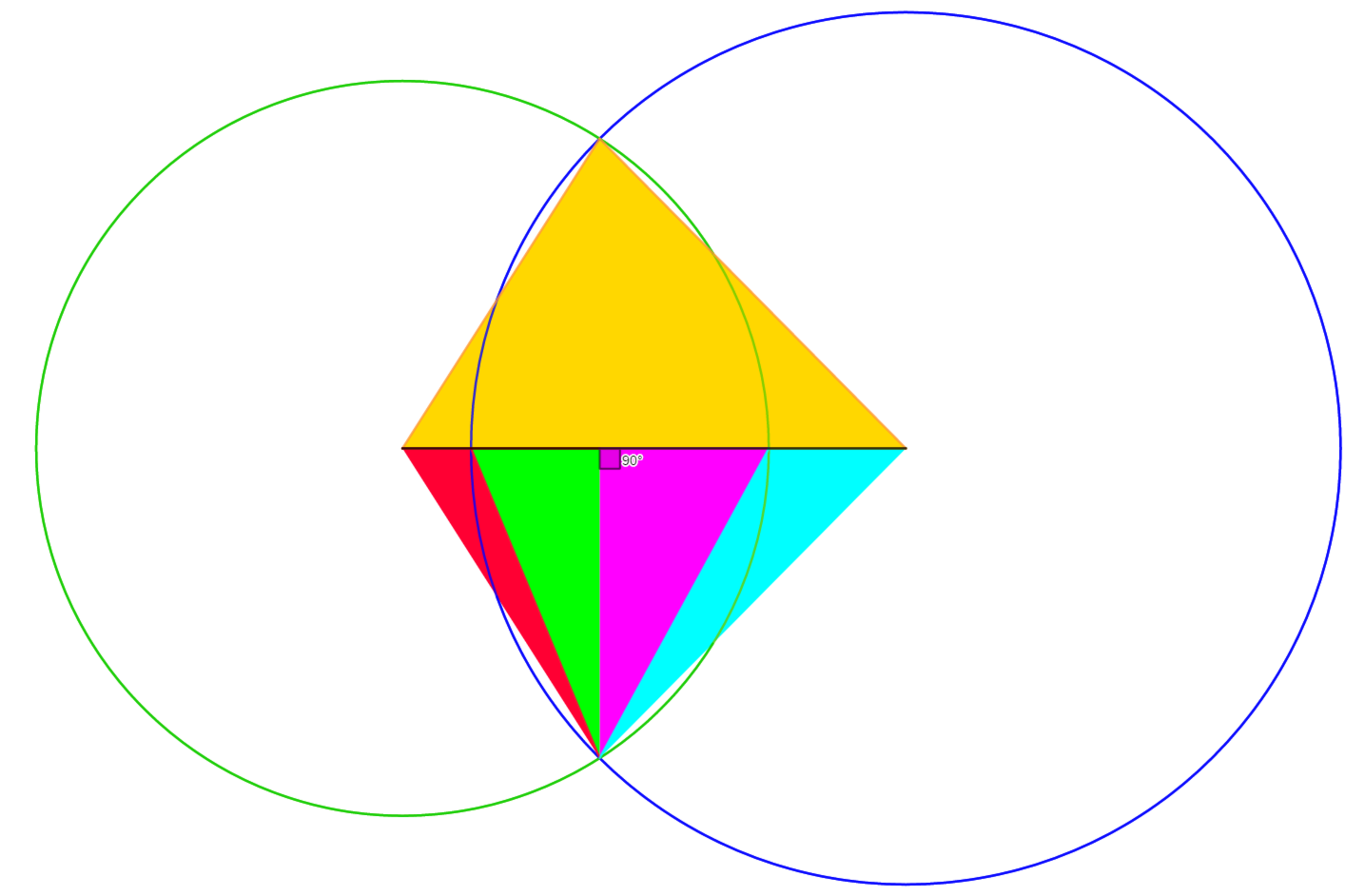
- The driagram shows a golden triangle with sides in arithmetic progression with the smallest side greater than the common difference between sides. The base (longest side) of the triangle is formed by joining the center of two circles. The vertex of the triangle, opposite to the base is the intersection point between the two circles. All sides of the triangle are integers.
- The altitudes of the golden triangle are 1 6 9 1 7 5 2 0 , 1 2 0 , 4 1 5 8 4 0
- The distance between the triangle's incenter and the triangle's circumcenter is 8 0 2 9 9 4 1
- Below the golden triangle, its reflection is partitioned in four smaller triangles
- We denote R the area of the red triangle
- We denote G the area of the green triangle
- We denote P the area of the purple triangle
- We denote B the area of the blue triangle
- Question : Evaluate B R + P G
- The answer can be expressed as b a where a and b are coprime positive integers.
-
Calculate
a
−
b
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
0 Helpful
0 Interesting
1 Brilliant
0 Confused
Very nice!
Valentin Duringer
- 10 months, 3 weeks ago
- We denote the sides of the golden triangle as : x − k , x , x + k with k being the common difference between sides.
- We use this useful property : r 1 = h 1 1 + h 2 1 + h 3 1 which allows us the solve for the inradius. : r = 4 0
- Then we use Euler's theorem to calculate the circumradius, knowing the value of the inradius and the distance between them : ( R − r ) ² = d ² + r ² < = > R = 8 0 6 9 2 9
- Now, we use two formulas : R = 4 ⋅ A r e a a ⋅ b ⋅ c and r = a + b + c 2 ⋅ A r e a
- Then : R ⋅ r = 2 ⋅ ( a + b + c ) a ⋅ b ⋅ c < = > 6 ⋅ x ( x − k ) ⋅ x ⋅ ( x + k ) = 2 6 9 2 9
- We obtain : x = k 2 + 2 0 7 8 7
- Since x is an integer, then k 2 + 2 0 7 8 7 has to be a perfect square and we find 5 values for x ; k and valid one is x = 1 4 6 and k = 2 3
- Then the sides of the triangles are 1 2 3 , 1 4 6 and 1 6 9
- The base a the red triangle has to be 1 6 9 − 1 4 6 = 2 3
- The base a the blue triangle has to be 1 6 9 − 1 2 3 = 4 6
- Using the altitude relative the base of the golden triangle and the pythagorean theorem we get :
- The base a the green triangle is 1 6 9 7 3 0 0
- The base a the green triangle is 1 6 9 9 6 0 0
- Since the 4 small triangles have the same height, the ratio of their areas is the ratio of the bases.
- B R + P G = 4 6 2 3 + 1 6 9 9 6 0 0 1 6 9 7 3 0 0 = 9 6 1 2 1
- 1 2 1 − 9 6 = 5
1 Helpful
1 Interesting
1 Brilliant
0 Confused
Let the lengths of the sides of the golden triangle in increasing order be c , d , 2 d − c . Let the center of the circle on left be O , that of the circle on the right be P , and the vertices of the different colored triangles on the line O P from O to P be A , B , C , and the common vertex of these triangles be D .
Then ∣ A C ∣ = 2 c − d
From the heights given, we can get the following relations
d = 1 2 3 1 4 6 c
2 d − c = 1 2 3 1 6 9 c
Since lengths of all the sides of the golden triangle are integers, their minimum values are 1 2 3 , 1 4 6 , 1 6 9
Then ∣ O B ∣ = 1 2 3 2 − ( 1 6 9 1 7 5 2 0 ) 2
= 1 6 9 1 1 1 8 7
⟹ ∣ B C ∣ = 1 6 9 9 6 0 0 , ∣ A C ∣ = 1 0 0 ,
∣ A B ∣ = 1 6 9 7 3 0 0 , ∣ O A ∣ = 1 6 9 3 8 8 7 ,
∣ C P ∣ = 4 6
Now, B R + P G = ∣ C P ∣ ∣ O A ∣ + ∣ B C ∣ ∣ A B ∣
= 2 1 + 9 6 7 3 = 9 6 1 2 1
So, a = 1 2 1 , b = 9 6 and a − b = 5