The Triangle Fit Just Nicely

Geometry Level 2

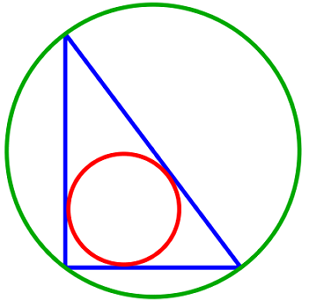
The above shows a triangle (in blue) with side lengths 3-4-5, that has both a circumscribed circle (in green) and a circle inscribed (in red) inside of it. Find the ratio of areas between the larger circle versus the smaller circle.

1.5^2

2.0^2

3.0^2

2.5^2

1 solution

Sam Bealing
Apr 17, 2016

As $3^2+4^2=5^2$ , the triangle is right-angled. Therefore, by the converse of Thale's theorem, the hypotenuse of the triangle is the diameter of the circle. This gives the radius of the green circle as $\frac{5}{2}=2.5$ .

The area of the triangle is $A=\frac{3 \times 4}{2}=6$ . Also we have that $A=s r$ where $r$ is the radius of the incircle and $s$ is the semiperimeter. This gives $r=\frac{A}{S}=\frac{6}{\frac{3+4+5}{2}}=1$ .

Therefore, the area of the circumcircle is $\pi \times 2.5^2$ and the incircle has area $\pi \times 1^2$ . The ratio of their areas is $2.5^2$

Moderator note:

Good clear explanation.

FYI I made several grammar and spelling edits to your solution for it to read smoother.

Calvin Lin Staff - 5 years, 1 month ago

The Triangle Fit Just Nicely

1 solution

Moderator note:

0 pending reports