This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
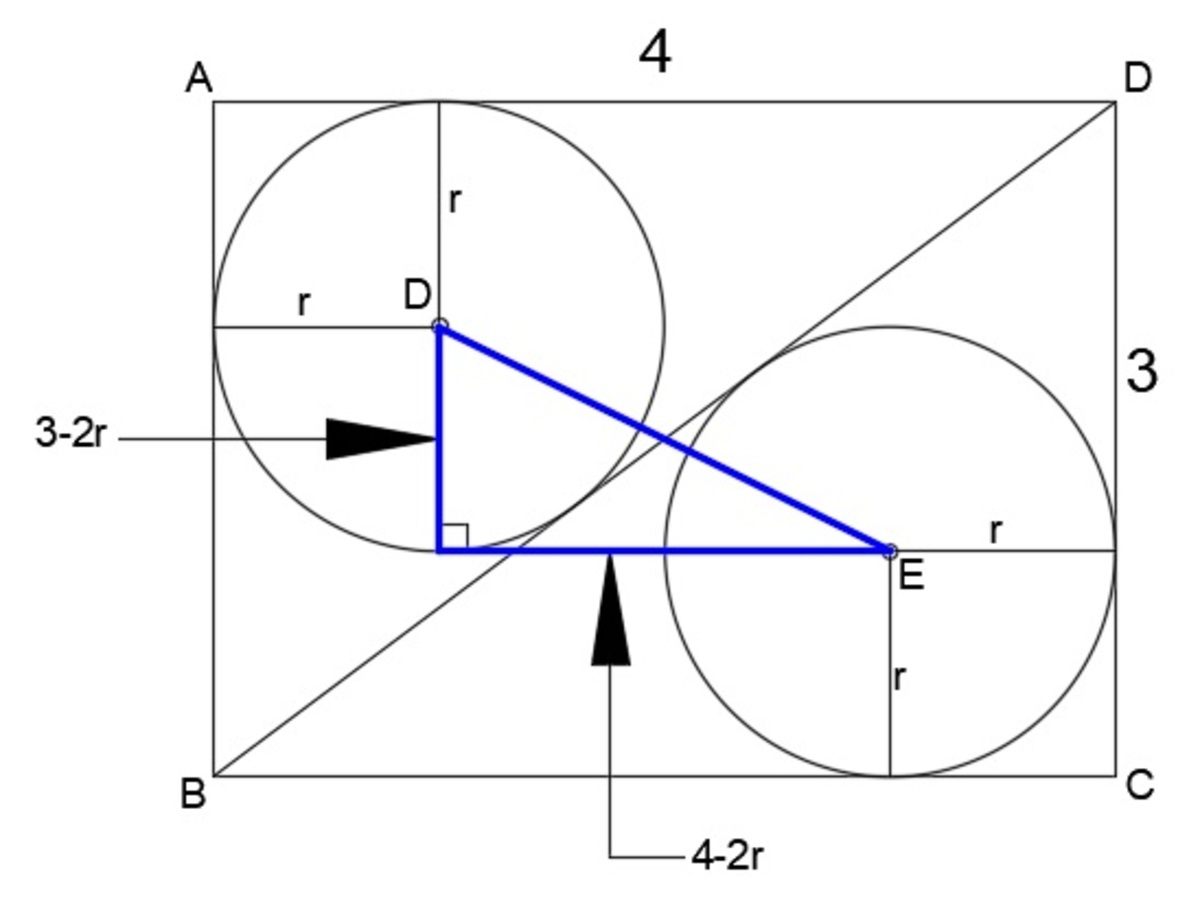
Consider my diagram.
tan ∠ D B C = 4 3 ⟹ ∠ D B C = tan − 1 ( 4 3 )
It follows that
∠ E B C = 2 1 ∠ D B C = 2 1 [ tan − 1 ( 4 3 ) ]
Then,
tan ∠ E B C = 4 − r r
tan 2 1 [ tan − 1 ( 4 3 ) ] = 4 − r r
By the use of a calculator,
3 1 = 4 − r r
r = 1
Apply pythagorean theorem on the blue right triangle, we have
( D E ) 2 = ( 3 − 2 r ) 2 + ( 4 − 2 r ) 2 = ( 3 − 2 ) 2 + ( 4 − 2 ) 2 = 1 + 4 = 5
Finally,
D E = 5 ≈ 2 . 2 3 6 0 6 7 9 7 8
Circles D and E are incenters of △ A B D and △ C D B . Setting B at the origin, we have A ( 0 , 3 ) , B ( 0 , 0 ) , C ( 4 , 0 ) , and D ( 4 , 3 ) .
So △ A B D 's incenter D is at ( a + b + c a x 1 + b x 2 + c x 3 , a + b + c a y 1 + b y 2 + c y 3 ) = ( 3 + 4 + 5 3 ⋅ 4 + 4 ⋅ 0 + 5 ⋅ 0 , 3 + 4 + 5 3 ⋅ 3 + 4 ⋅ 0 + 5 ⋅ 3 ) = ( 1 , 2 ) , and △ C D B 's incenter E is at ( a + b + c a x 1 + b x 2 + c x 3 , a + b + c a y 1 + b y 2 + c y 3 ) = ( 3 + 4 + 5 3 ⋅ 0 + 4 ⋅ 4 + 5 ⋅ 4 , 3 + 4 + 5 3 ⋅ 0 + 4 ⋅ 3 + 5 ⋅ 0 ) = ( 3 , 1 ) .
The distance between D ( 1 , 2 ) and E ( 3 , 1 ) is d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 = ( 3 − 1 ) 2 + ( 1 − 2 ) 2 = 5 ≈ 2 . 2 3 6 .
Radius of the circles is 1. Horizontal distance between centers is 2, vertical distance is 1. D E = 5 .
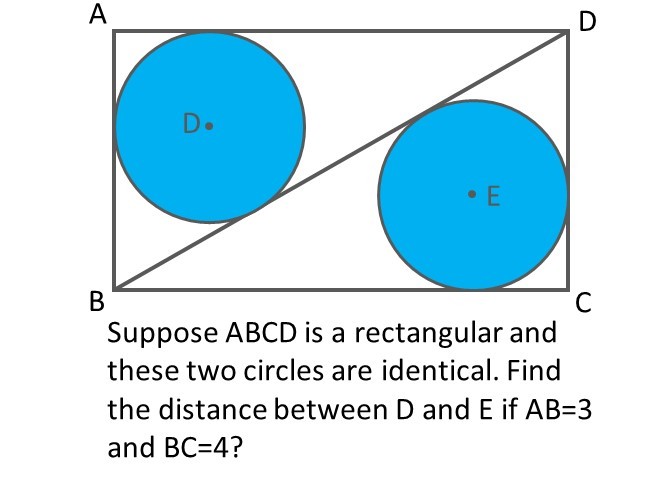
Using the formula r ∗ s = [ △ A D B ] where s is the semiperimeter, r is the radius of the triangle's incircle and [ △ A D B ] is the area of △ A D B , we can solve for the radius. Because B D = 5 by the Pythagorean Theorem, s = 2 3 + 4 + 5 = 6 . Furthermore, [ △ A D B ] = 2 3 ∗ 4 = 6 . Thus, solving for the radius of either incircle, we get r = s [ △ A D B ] = 6 6 = 1 Then, by realizing that both triangles are identical, D E must be 1 apart vertically and 2 apart horizontally. Thus, by the Pythagorean Theorem. 1 2 + 2 2 = 5 ≈ 2 . 2 3 6