The Ultimate Snowflake
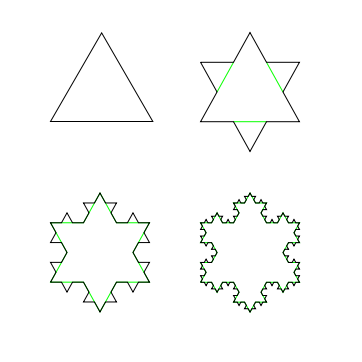 An ultimate snowflake (Koch Snowflake) is formed when each side of an equilateral triangle is divided in
3
equal parts, and a new equilateral triangle is constructed in the middle part. Repeat this step infinitely for each side of the polygon formed. Given that the side of the initial equilateral triangle of one such ultimate snowflake is 5 units, find the square of the area of the polygon (after repeating the above process infinitely).
An ultimate snowflake (Koch Snowflake) is formed when each side of an equilateral triangle is divided in
3
equal parts, and a new equilateral triangle is constructed in the middle part. Repeat this step infinitely for each side of the polygon formed. Given that the side of the initial equilateral triangle of one such ultimate snowflake is 5 units, find the square of the area of the polygon (after repeating the above process infinitely).
The answer is 300.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I must admit that approach to the problem is simply elegant. cheers!!!
Nice solution! :) Haha I did a much longer way!
you're aweosme
We will solve this problem for general initial side length s 0 .
The initial area A 0 is given by the equilateral triangle area formula to be $$A 0 = \frac{\sqrt{3}}{4}s 0^2.$$ Each iteration, the total area is increased by the area of the new triangles added to the polygon. The number of triangles added is simply the number of sides before that iteration. The number of sides σ n of the polygon is multiplied by four every iteration, that is $$\sigma n = 4\sigma {n-1}.$$ This a simple geometric relation, so we have $$\sigma n = 3 \cdot 4^n.$$ The side lengths s n of the triangle are divided by three every iteration, so we have $$s n = \frac{1}{3}s {n-1}.$$ This also a geometric relation, so we have $$s n = s 0 \left(\frac{1}{3}\right)^n.$$ So the amount of area added at the n th iteration a n is the number of triangles added times the area of each of the triangles, i.e., $$a n = \sigma {n-1}\frac{\sqrt{3}}{4}(s n) ^2$$ $$=3\cdot4^{n-1}\frac{\sqrt{3}}{4}\left(s 0 \left( \frac{1}{3}\right)^n\right)^2$$ $$=\frac{3\sqrt{3}}{16}s 0^2\left( \frac{4}{9} \right)^n.$$ The total area after n iterations A n is the initial area A 0 plus the sum of all of the areas added. That is $$A n = A 0 + \sum\limits {i=1}^{n} a i$$ $$=\frac{\sqrt{3}}{4}s 0^2 + \sum\limits {i=1}^{n} \frac{3\sqrt{3}}{16}s 0^2\left( \frac{4}{9} \right)^i$$ $$=\frac{\sqrt{3}}{4}s 0^2 +\frac{3\sqrt{3}}{16}s 0^2 \sum\limits {i=1}^{n} \left( \frac{4}{9} \right)^i.$$ The area of the Koch Snowflake A is simply the limit (if it exists) of A n as n → ∞ : $$A=\lim {n \to \infty} A n$$ $$= \lim {n \to \infty} \left( \frac{\sqrt{3}}{4}s 0^2 +\frac{3\sqrt{3}}{16}s 0^2 \sum\limits {i=1}^{n} \left( \frac{4}{9} \right)^i\right)$$ $$= \frac{\sqrt{3}}{4}s 0^2 +\frac{3\sqrt{3}}{16}s 0^2 \sum\limits_{i=1}^{\infty} \left( \frac{4}{9} \right)^i.$$ The sum is a geometric sum with first term 4 / 9 and common ratio 4 / 9 , so it converges to 1 − 4 / 9 4 / 9 = 5 4 .
So we have $$A=\frac{\sqrt{3}}{4}s 0^2 +\frac{3\sqrt{3}}{16}s 0^2 \left( \frac{4}{5} \right),$$ which simplifies to $$A=\frac{2\sqrt{3}}{5}s_0^2.$$ So, in our case, when s 0 = 5 , we have $$A=10\sqrt{3},$$ whose square is $$A^2=\boxed{300}.$$
Let us assume the initial trianle side as 's', at first step 3 new triangles' are added on each side with side 3 s and in the second step a new trianlge with side 3 2 s is added on each of 4 × 3 sides. This is repeated infinitely, the n t h time repeatition will have a side of 3 n s and total number of sides triangles will be 3 × 4 n − 1 .
area of equilateral triangle is 4 3 × s 2
area of polygon will be 4 3 × s 2 [ 1 + 3 2 3 + 3 4 4 × 3 + 3 6 4 2 × 3 + 3 8 4 3 × 3 . . . . . . . . . . . ]
= 4 3 × s 2 [ 1 + 3 1 + 3 3 2 2 + 3 5 2 4 + 3 7 2 6 . . . . . . . . . . . ]
= 4 3 × s 2 [ 1 + 1 − 3 2 2 2 1 / 3 ]
= 4 3 × s 2 [ 1 + 5 3 ]
= 5 2 × 3 × s 2
When s = 5 , area of the polygon will be 1 0 × 3
square of the area is 300
First notice that for each generation of triangles, the area of each triangle decreases by a factor of 9 1 . Also, the number of triangles in each generation increases by a factor of 4 (in the first generation there are 3 more, then 1 2 , 4 8 , … ). Therefore, the total area for each generation of triangles increase by a factor of 9 4 . Let the area of the original triangle be a , then we have the area of the snowflake, A is, A = a + 3 1 a + 2 7 4 a + 2 4 3 1 6 a + … First we evaluate the geometric series, 3 1 a + 2 7 4 a + 2 4 3 1 6 a + … This is equal to 1 − 9 4 3 1 a = 5 3 a Hence the total area is A = 5 8 a . Now a = 4 2 5 3 Hence the total area, A is, A = 5 8 ⋅ 4 2 5 3 = 1 0 3 ⇒ A 2 = 3 0 0