The Uncomfortable Square

Geometry Level 3

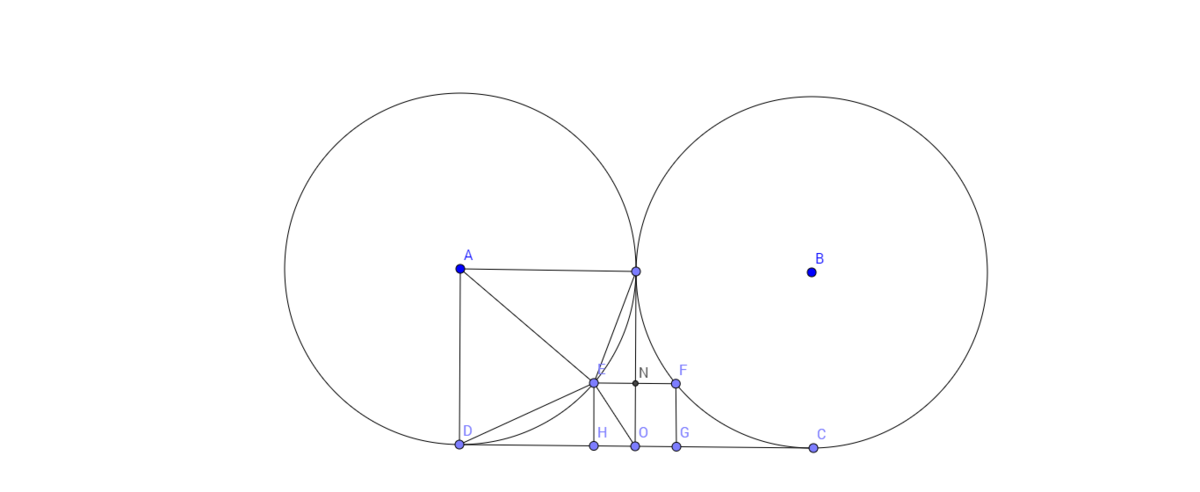
There are two circles of equal radius $1$ that are centered at points $A$ and $B,$ respectively, and externally tangent to each other. A tangent $DC$ is drawn to both circles, and a square $EFGH$ fits between the circles such that points $G$ and $H$ lie on the line segment $DC.$

Find the side length of the square.

The answer is 0.4.

3 solutions

Vishwash Kumar Γξω
Nov 19, 2016

.

I knew there was a easier solution. Must say nice observation hats off to u +1

Ayush G Rai - 4 years, 6 months ago

Oh that is even not a square hahaha how could it be uncomfortable . Get a cushion below it if it is feeling uncomfortable Hahahahaha

Vishwash Kumar ΓΞΩ - 4 years, 6 months ago

Its an indirect way of saying.

Ayush G Rai - 4 years, 6 months ago

Ayush G Rai
Nov 19, 2016

A Former Brilliant Member
Apr 2, 2017

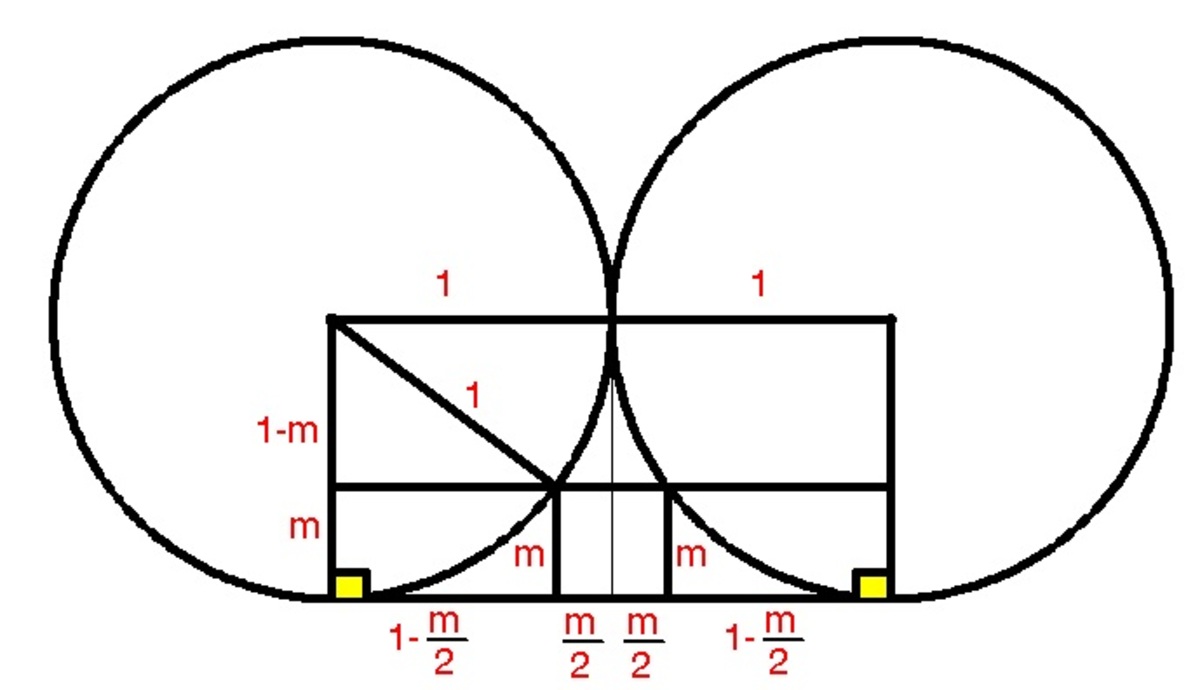let $m$ be the side length of the square

using Pythagorean Theorem, we have

$1^2 = (1-m)^2 + (1 - \frac{m}{2})^2$

after expanding and simplifying, we get

$m^2 - 2.4m + 0.8$

Using the quadratic formula to solve for $m$ , we get

$m = 2$

$m = 0.4$

Since radius is $1$ , $m$ must be lesser than $1$ , so $\boxed{\large\color{#D61F06}m = 0.4}$