The unique rectangle on a cubic
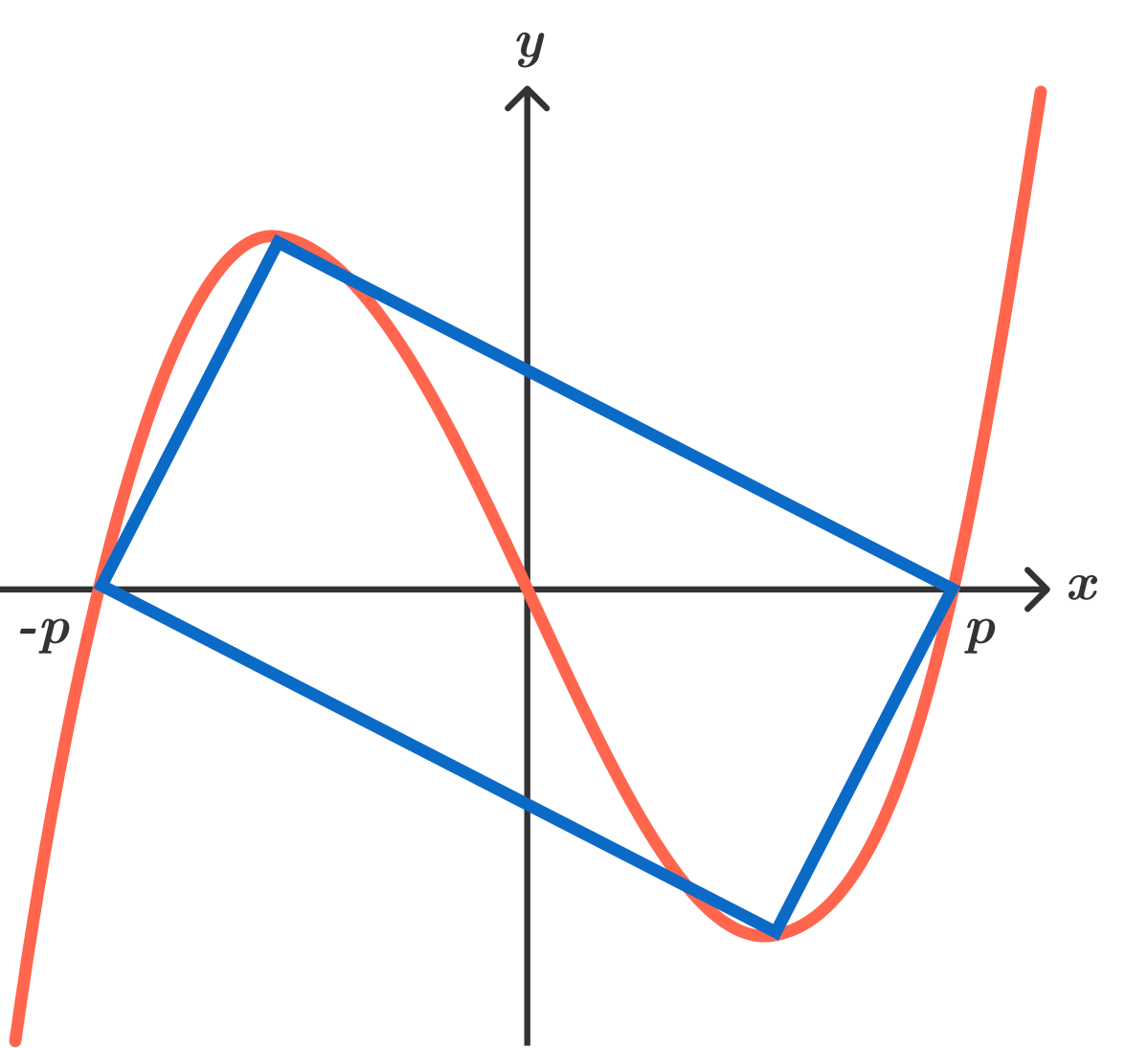
From a cubic equation with roots and , a rectangle, with two of its opposite vertices touching the two non-zero -intercepts and the other two vertices touching two other points on the curve, can be constructed.
If there is only one possible length to width ratio of the rectangle which can be expressed as
in the simplest form, what is
?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the roots of the cubic are 0 , p and − p , its equation can be expressed in the form y = a x ( x − p ) ( x + p ) = a x ( x 2 − p 2 ) where a is a constant.
Now, the angle subtended by the diameter of a circle at the circumference is always a right angle. Therefore, since the angles in a rectangle are right angles, the vertices of the rectangle at C and D must lie on a circle with diameter AB, i.e. x 2 + y 2 = p 2 .
Equating the equation of the circle with the equation of the cubic:
x 2 + y 2 y 2 [ a x ( x 2 − p 2 ) ] 2 a 2 x 2 ( x 2 − p 2 ) 2 a 2 x 2 ( x 2 − p 2 ) a 2 x 4 − a 2 p 2 x 2 + 1 = p 2 = p 2 − x 2 = p 2 − x 2 = − ( x 2 − p 2 ) = − 1 = 0
This is a quadratic equation in terms of x 2 . Now, notice how the circle intersects the cubic at C and D and also another pair of points. For there to be only one possible rectangle, there must be only two intersections (which by the symmetry of the rectangle must be at x = n and x = − n for some number n and are therefore the solutions to x 2 = n 2 ), and so the quadratic above must have equal roots. This means the discriminant equals zero.
Δ = B 2 − 4 A C ∴ ( a 2 p 2 ) 2 − 4 ( a 2 ) ( 1 ) a 4 p 4 a 2 a = 0 = 0 = 4 a 2 = p 4 4 = p 2 2 ( a , p > 0 WLOG )
Now we can complete the quadratic equation and find the coordinates of C and D.
p 4 4 x 4 − p 4 4 p 2 x 2 + 1 4 p 4 x 4 − 4 p 2 x 2 + 1 ( 2 p 2 x 2 − 1 ) 2 2 p 2 x 2 x 2 x ∴ y ∴ C ( − 2 p , 2 p ) , = 0 = 0 = 0 = 1 = 2 p 2 = ± 2 p = ± p 2 2 2 p ( 2 p 2 − p 2 ) = ∓ 2 p D ( 2 p , − 2 p )
Finally, we simply need to find the ratio between the length and width of the rectangle. Draw a perpendicular from C to meet the x-axis at M, as in the diagram. Now, using the coordinates of C, C M = 2 p and A M = p + p 2 . The right triangle ACM is similar to triangle ABC, since both have a right angle and also a common angle at B. Therefore, the ratio of the length to the width of the rectangle, i.e. B C A C , equals C M A M = p p + p 2 = 1 1 + 2 . Therefore the answer is 1 + 2 + 1 = 4