The unknown vector

Let's first of all find the value of $|\vec{P}|$ . $|\vec{P}| = \sqrt{a^{2}+4b^{2} + 4ab\Big( \dfrac{-3b}{2a}\Big) }$ $|\vec{P}| = \sqrt{a^{2} - 2b^{2}}$

Now we can check the modulus of each options. The one which matches with the above value will be the answer.

So let's check the modulus of $(\vec{a}+\vec{b})$ . $|\vec{a} + \vec{b}| = \sqrt{a^{2} + b^{2} + 2ab\Big(\dfrac{-3b}{2a}\Big) }$ $|\vec{a} + \vec{b}| = \sqrt{a^{2} -2b^{2}}$ Hence Option $(C)$ is correct.

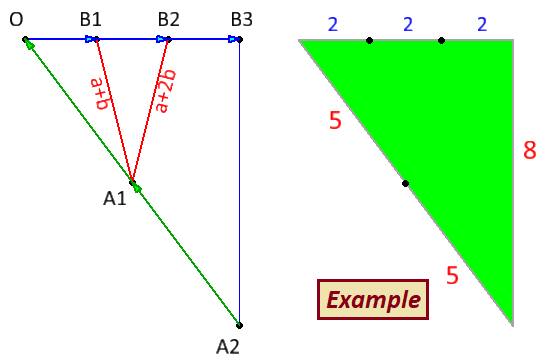
One can also take a visual approach: The given cosine $(\frac{-3b}{2a})$ suggests a right angle formed with side 3b and hypotenuse 2a! (One can imagine b=2 and a=5 to visualize a 6,8,10 right triangle) A similar right triangle of half the size is formed by vectors $\vec a$ and $\vec {1.5b}$ Adding or subtracting $\vec {0.5b}$ will give two symmetric points B1 and B2 Giving equal lengths A1B1 and A1B2, which are $\vec a + \vec b$ and $\vec a + \vec {2b}$ respectively!