The Vitruvian Triangle
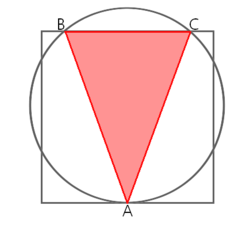A square and circle with equal areas are placed in such a way that both intersected in some points like Vitruvian Man of Leonardo Da Vinci. One of the intersections is point
A
, located exactly on middle of square side (see illustration). Two other points, called
B
and
C
, are chosen from intersection points so that
ABC
triangle can be formed. If the area of square (or circle) is one unit, what is the area of
ABC
triangle?
(Enter approximation up to 3 digits on answer box)
The answer is 0.358.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Notice that the altitude of the triangle is 1 so the area is equal half BC. Let M be the midpoint of BC and let O be the centre of the circle. Then O C = π 1 as the circle has area 1. Now O X = A X − O A = 1 − π 1 . Now using Pythagoras' Theorem ( X C ) 2 = π 1 − ( 1 − π 1 ) 2 = π 2 − 1 ∴ A r e a ( A B C ) = X C = π 2 − 1 ≈ 0 . 3 5 8