The volume of a solid of revolution of the area between y = x and y = y^2 and 0<=x<=1
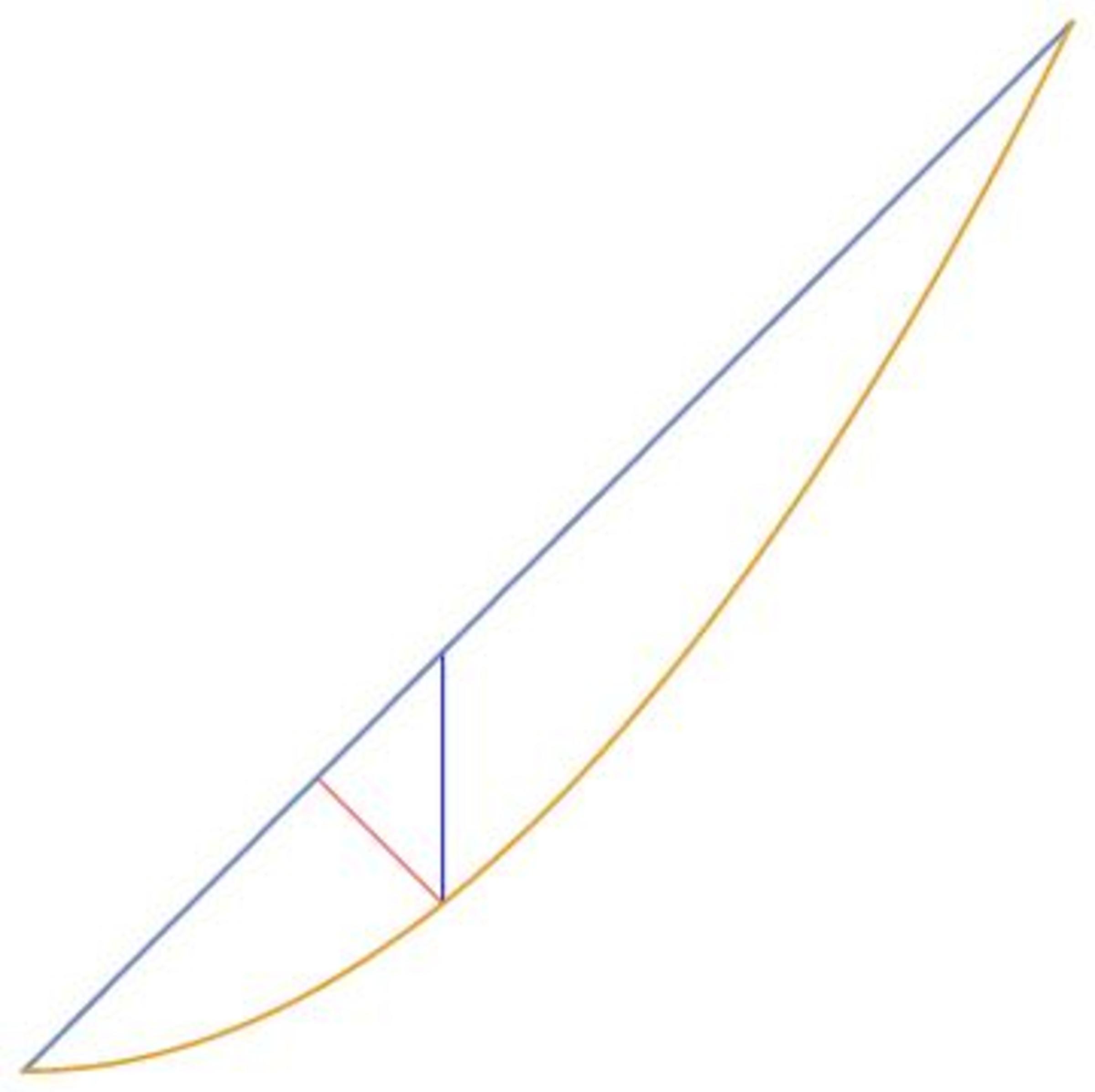
The title of the problem is the problem description. The graph is intended as an aid for those whom an image helps to understand the situation. The graph was deliberately left unannotated as determining the annotations is part of the solution.
Find the volume of a solid of revolution of the area between y = x and y = y^2 and 0<=x<=1
The axis of revolution is the line.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I have solved this problem several different ways : rotating the y = x line to the x axis (a very messy integral, but solvable), integration by cones (resembles integration by "washer" using the area of the side of cone with a side equal to x − x 2 ) or by the integration by displaced "washer" (using the area of the base of the aforementioned cone). It turns out, I feel \ that the last method is the simplest.
2 π ∫ 0 1 ( x 4 − 2 x 3 + x 2 ) d x is 2 π ∣ 5 x 5 − 2 x 4 + 3 x 3 ∣ x = 0 1 is 3 0 2 π ( 6 − 1 5 + 1 0 ) is 3 0 2 π
0 . 0 6 9 8 1 3 1 7 0 0 7 9 8