The Wet Condenser?!
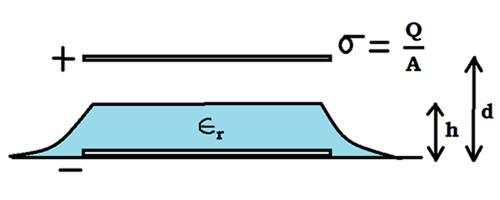 A Parallel Plate Condenser is charged with a surface charge density
σ
=
A
Q
. Due to a pipe leakage, water flows in. It is observed that the water surface
rises
to a height
h
above the bottom plate.
A Parallel Plate Condenser is charged with a surface charge density
σ
=
A
Q
. Due to a pipe leakage, water flows in. It is observed that the water surface
rises
to a height
h
above the bottom plate.
Find the height h (in cm ) to which the water level rises.
Details and Assumptions:
∙
ϵ
r
=
8
0
∙
ρ
w
a
t
e
r
=
1
0
0
0
K
g
/
m
3
∙
g
=
9
.
8
m
/
s
2
∙
σ
=
2
μ
C
/
m
2
The answer is 0.002277.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Isnt frinding field the cause for the rise?
The entire system should assume the configuration which minimises the entire potential energy which gives the answer as given in the question that is 0.002277cm
If we neglect all friction types, the water will reach height h, and then undergo oscillatory motion and stop at the height h/2, after a while it will undergo damped oscillatory motion and stop eventually at the point where mg = F , so shouldn't you have taken h/2 instead of h? :)
The electric field due to the induced charges(these charges are induced on the top and bottom surfaces of the dielectric) superimposes with the already present electric field and reduces it by a factor ϵ r . The magnitude of induced surface charge density will be:
σ i n d u c e d = ϵ r σ ( ϵ r − 1 )
Hence, putting ϵ r = 8 0 we get σ i n d u c e d = 8 0 7 9 σ
The top surface of water(dielectric) will rise till the net force due to the following is zero:
1. The weight of the water (which is pulling down the top surface)
2. Electrostatic force of attraction due to the charge induced on the lowermost surface of the dielectric (which is again pulling down the top most surface down)
3. And the electrostatic force acting in the upward direction on the top layer of water due to the electric field of the condenser.
Therefore, ( A F 1 ) due to condenser = ( A V ρ w a t e r g ) due to weight of water + ( A F 2 ) due attraction between induced layer of charges on the dielectric
( ϵ 0 σ ) ∗ σ i n d u c e d = h ρ g + ( 2 ϵ 0 σ i n d u c e d ) ∗ σ i n d u c e d
Now after putting the values for
σ = 2 ∗ 1 0 − 6 C ;
σ i n d u c e d = 8 0 7 9 σ ;
ρ = 1 0 0 0 k g / m 3 ;
g = 1 0 m / s − 2
we get the answer as:
h = 2 . 2 7 ∗ 1 0 − 3 c m
Energy before water started to flows in is:
E 1 = 2 C 1 q 2 Where C 1 = d e 0 S
When the water in steady state we have two capacitator
C 2 = h e 0 e r S and C 3 = d − h e 0 S
each with charge q
They have energies E 2 = 2 C 2 q 2 and E 3 = 2 C 3 q 2
Also the water has potentional energy E p = 2 m g h
By conversation law we now E 1 = E 2 + E 3 + E p and finally we get :
h = ( S q ) 2 ∗ ( \ro g ϵ o ) ( 1 − ϵ r 1 )