The Witch of Agnesi

Geometry Level 3

"The Witch of Agnesi" is a parametrically defined curve researched by Maria Agnesi in 1748.

What is the x ( t ) x(t) part of this parametric definition?

x ( t ) = ? ; y ( t ) = 2 sin ⁡ 2 ( t ) ; \hspace{20mm} x(t) = \ ?; \hspace{3mm} y(t) = 2\sin^2(t) \hspace{1mm};\hspace{3mm} for t = ( 0 , π ) t = (0, \pi)

Details:

x = 2 sin ⁡ ( t ) x=2\sin(t) x = 2 cot ⁡ ( t ) x=2\cot(t) x = cot ⁡ 2 ( t ) x=\cot^2(t) x = cos ⁡ ( t ) x=\cos(t)

Zandra Vinegar by Zandra Vinegar

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Zandra Vinegar Staff
Oct 8, 2015

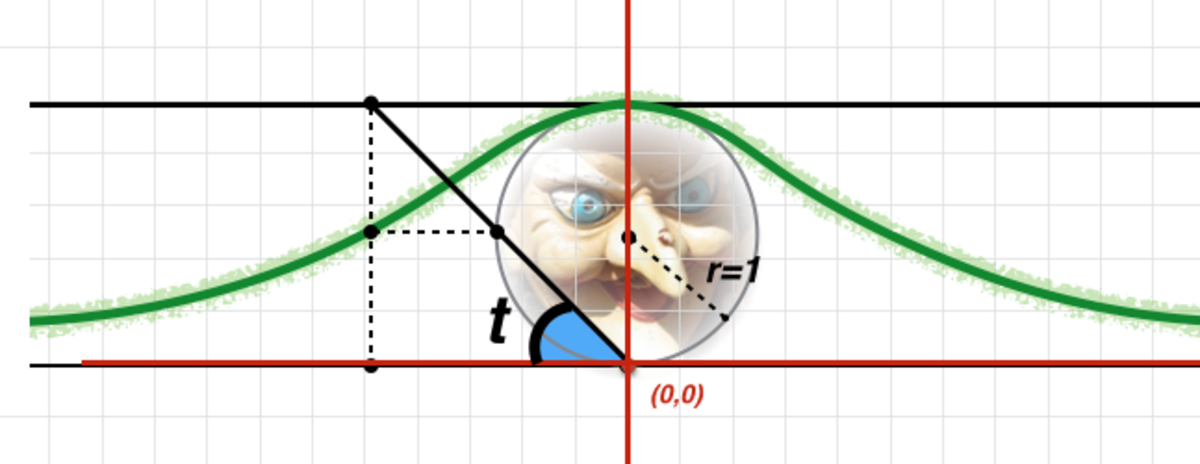
Since the circle has radius 1, the horizontal line above the circle must be y = 2 ( i n p u r p l e ) y=2 \hspace{2mm} \color{#69047E}{(in \hspace{2mm} purple)}

The line that begins at the bottom of the circle, at angle t t with the horizontal axis has slope = s i n ( t ) c o s ( t ) = t a n ( t ) = \frac{sin(t)}{cos(t)} = tan(t) and y-intercept 0. So the equation for the line is: y = t a n ( t ) x + 0 ( i n o r a n g e ) y = tan(t) \hspace{2mm} x + 0 \hspace{2mm} \color{#EC7300}{(in \hspace{2mm} orange)}

The x-coordinate of the intersection of these two lines ( o r a n g e a n d p u r p l e ) \color{#EC7300}{orange} \hspace{2mm} and \hspace{2mm} \color{#69047E}{purple}) defines the x-coordinate of the Witch of Agnesi curve ( g r e e n ) \color{#20A900}{green}) . So we have that 2 = t a n ( t ) x 2 = tan(t) \hspace{2mm} x

Solving for x x yields: x = 2 c o t ( t ) x = 2cot(t)

2 Helpful 0 Interesting 0 Brilliant 0 Confused

This curve is pretty awesome. It is now known to have applications in physics modeling the spectral line distribution of optical lines and x-rays, as well as the amount of power dissipated in resonant circuits.

Zandra Vinegar Staff - 5 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...