The world of work - 3.part(correct version)
Your second mission:
On your first raid, you got into a duel with two other people. All of you have only one gun. The rules of this duel are rather peculiar: the duelists do not all shoot simultaneously, but take turns. A can fire at B, B can fire at C, and C can fire at A; the cycle repeats until there is a single survivor. If you hit your target, you'll fire the next person on your next turn.
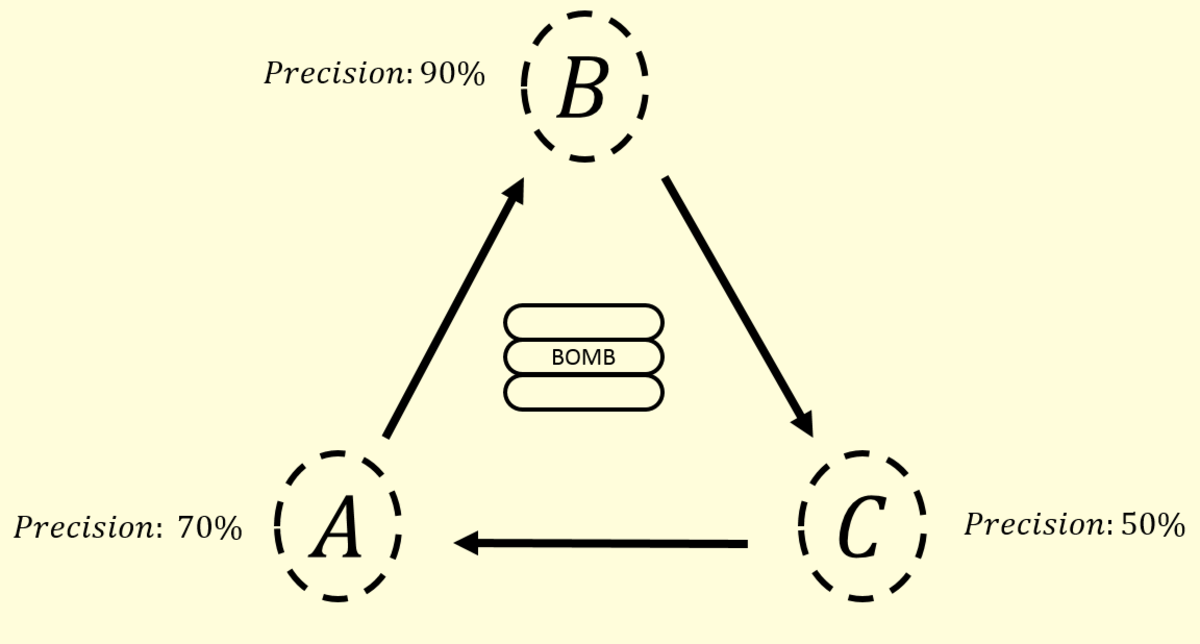
You are A. What are your chances of surviving? If none of you shoot, you will explode. Give your answer in % and round up!
Report room - Here you will see the other parts of the series too.

The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
You can see these things:
So if you shoot your chances: p 1 ( A ) = 0 . 7 p ( C A ) + 0 . 9 ( 1 − 0 . 7 ) p ( A B ) + ( 1 − 0 . 7 ) ( 1 − 0 . 9 ) p 1 ( A ) Where p(CA) is the probability to win a duel with C, if C is the first shooter, and p(AB) where you are the first shooter. p ( C A ) p ( A B ) = 0 . 7 ( 1 − 0 . 5 ) + ( 1 − 0 . 7 ) ( 1 − 0 . 5 ) p ( C A ) = 0 . 7 + ( 1 − 0 . 7 ) ( 1 − 0 . 9 ) p ( A B ) So: p 1 ( A ) = 1 − 0 . 3 ⋅ 0 . 1 0 . 7 1 − 0 . 3 ⋅ 0 . 5 0 . 7 ⋅ 0 . 5 + 0 . 9 ⋅ 0 . 3 1 − 0 . 3 ⋅ 0 . 1 0 . 7 = 1 − 0 . 0 3 0 . 7 1 − 0 . 1 5 0 . 3 5 + 0 . 2 7 1 − 0 . 0 3 0 . 7 = 0 . 9 7 0 . 8 5 0 . 2 4 5 + 0 . 9 7 0 . 1 8 9 ≈ 5 0 % And if you don't shoot, then B won't shoot too and C will shoot you, until he don't kill you, so your chances 0% in this case. 5 0 % > 0 % ⇒ 5 0 %
Here is my C++ code:
Output: