The Wrecked Rectangle
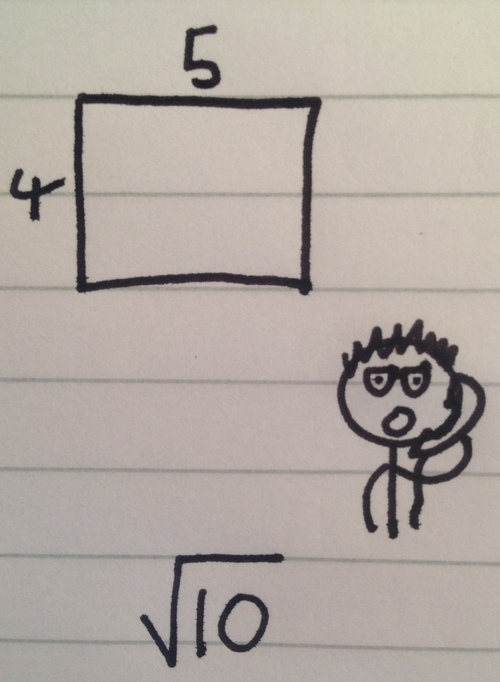 A mathematician has a rectangle of length 5, width 4. His physicist friend phones him up with a problem involving this rectangle, but the sides have been scaled down by a factor of
1
0
. The physicist asks the mathematician to determine the area of the rectangle, for her to use in her calculations.
A mathematician has a rectangle of length 5, width 4. His physicist friend phones him up with a problem involving this rectangle, but the sides have been scaled down by a factor of
1
0
. The physicist asks the mathematician to determine the area of the rectangle, for her to use in her calculations.
The mathematician does the calculation, but decides to test the physicist and gives his answer in the form:
x y x y x y x . . . .
where x and y are positive integers.
What is the sum of all possible values of x and y that the mathematician could have given to the physicist?
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The real question is: how did the physicist manage to figure out the second question if he couldn't figure out the first?
I also edited the wording because the original wording didn't make sense in the second part (where the physicist gave two answers). This is because the mathematician, not the physicist, is the one who gives two possible questions; after giving one of the two questions, the physicist can only give the one answer back.
Log in to reply
Thanks for that :) the simplification makes it much better! I think I sort of rushed the ending after having done the work for the first bit.
Thats good
I think the set of all possible values for x and y is {1, 2, 8} so the total should be 11. Not sure I like the end wording of the problem.
The area is ( 1 0 ) 5 ∗ ( 1 0 ) 4 = 2
Let the expression be denoted by z , therefore we have that:
z = 2
⇒ z 2 = x y z = x 2 y = 4
⇒ 2 x 2 y = 1 6
⇒ x 2 y = 8 = 2 x 2 y
x 2 y − 2 x 2 y = 0 ⇒ x ( x y − 2 2 y ) = 0
x = 0 ⇒ x y − 2 2 y = 0
x y = 2 2 y ⇒ x 2 y 2 = 8 y
x 2 y 2 − 8 y = 0 ⇒ y ( x 2 y − 8 ) = 0
y = 0 ⇒ x 2 y = 8 , { x , y } ⊂ Z +
Therefore x 2 must be a square factor of 8 so x 2 = 1 , 4
x 2 = 1 ⇒ x = 1 , y = 8
x 2 = 4 ⇒ x = 2 , y = 2
1 + 8 + 2 + 2 = 1 3
Aren't the best mathematicians crazy ;)
Let r ( ) be square root:
Let z = [4/ r (10)] x [5/ r (10)] = 2;
(z^2/ x)^2/ y = z
=> z^3 = x^2 y
=> 8 = x^2 y
(x, y) = (1, 8) or (2, 2) only.
Check by substitution:
r (r (8 r (r (8 r (r (8 r (1))))))) = 1.978+ and
r (2 r (2 r (2 r (2 r (2 r (2 r (2))))))) = 1.978+
Answer = 1 + 8 + 2 + 2 = 13.
Crazy mathematician however.
In order to scale it down, the lengths must be divided by 1 0 (or the area divided by 10).
This gives: 1 0 5 × 1 0 4 = 2 for the area.
Therefore: 2 = x y x y x . . .
Notice the embedded equation and this can be reduced to the form:
2 = x y ( 2 )
4 = x 2 y
x 4 = 2 y
x 2 1 6 = 2 y
x 2 y = 8
From this it can be worked out that the only values for x and y are 1,8,2 & 2 and therefore the answer is 13 [The factors of 8 are 1,2,4 & 8. With 1 and 4 both being square numbers these both fit into the form x 2 y = 8 ] =)