There are 2 paths
This is a question from the UKMT Maclaurin Olympiad, in which the solution is pretty straightforward as well! There are 2 (or more) ways of approaching this problem, but you could only rely on basic geometry!
Put your answer as a decimal, for example 0.4, 0.025 etc
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
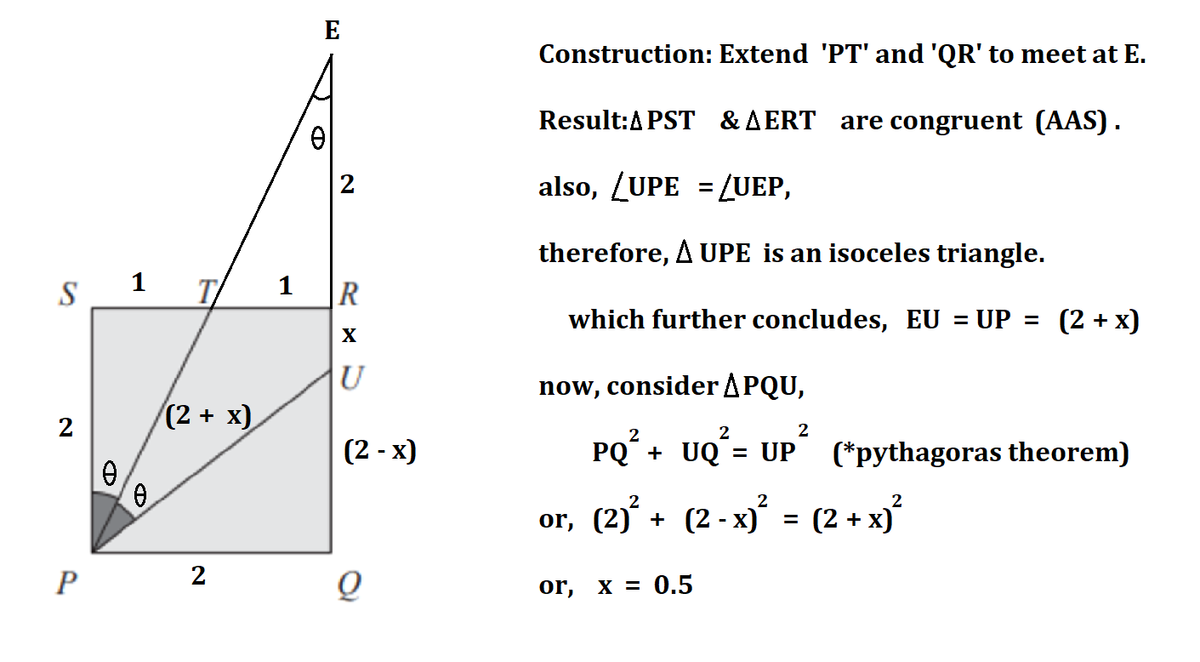
Let ∠ S P T = ∠ T P U = θ . Then ∠ U P Q = 9 0 ∘ − 2 θ , and
∣ U R ∣ = ∣ R Q ∣ − ∣ P Q ∣ tan ∠ U P Q = 2 − 2 tan ( 9 0 ∘ − 2 θ ) = 2 − 2 cot ( 2 θ ) = 2 − 2 × 2 tan θ 1 − tan 2 θ = 2 − 2 × 2 × 2 1 1 − 4 1 = 2 1 = 0 . 5 Note that tan θ = 2 1
Let ∠ S P T = ∠ T P U = α . Then tan α = 2 1 , tan ( 2 α ) = 2 − ∣ U R ∣ 2 = 1 − 4 1 2 × 2 1 = 3 4 ⟹ ∣ U R ∣ = 2 1 = 0 . 5 .
i couldnt find where to post a solution. i find a way without trigonometry. lets build perpendicular from T to PU and call it O. PTU and OTU are similar so OU/TU=TU/PR -> sqrt5 OU=TU. TU^2=TR^2+RU^2, which is (sqrt5 OU)^2=OU^2+1 -->OU=RU=0,5
Log in to reply
How do you know that △ P T U and △ O T U are similar?
Log in to reply
nice point! he needs to show that..
triangle PTO & triangle PTS are congruent by (ASA) congruency, so by (CPCT) ST = OT = 1. Again consider quad(PSTO) it's a cyclic quad... so (angle SPO) = (angle OTR) = 2 theta... similarly triangle OTU and triangle RTU are congruent by (RHS) congruency … which further gives (angle OTU) = (angle RTU) = theta ..by CPCT.
Now, (angle PTU) = angle PTO + angle RTU = (90 - theta) + theta = 90... which makes PTU and OTU similar triangles...