There Are 3 Interior Angles! Which One?

Geometry Level 1

The above shows an isosceles triangle with its apex at the center of a circle and its base tangent to the circle. If one of the isosceles angles of the triangle is 3 0 ∘ 30^\circ , then the area of the overlapping region bounded by the triangle and the circle is __________ \text{\_\_\_\_\_\_\_\_\_\_} times the area of the circle.

1 2 \frac12 1 3 \frac13 1 4 \frac14 1 5 \frac15

View wiki
Pi Han Goh by Pi Han Goh , 30, Malaysia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

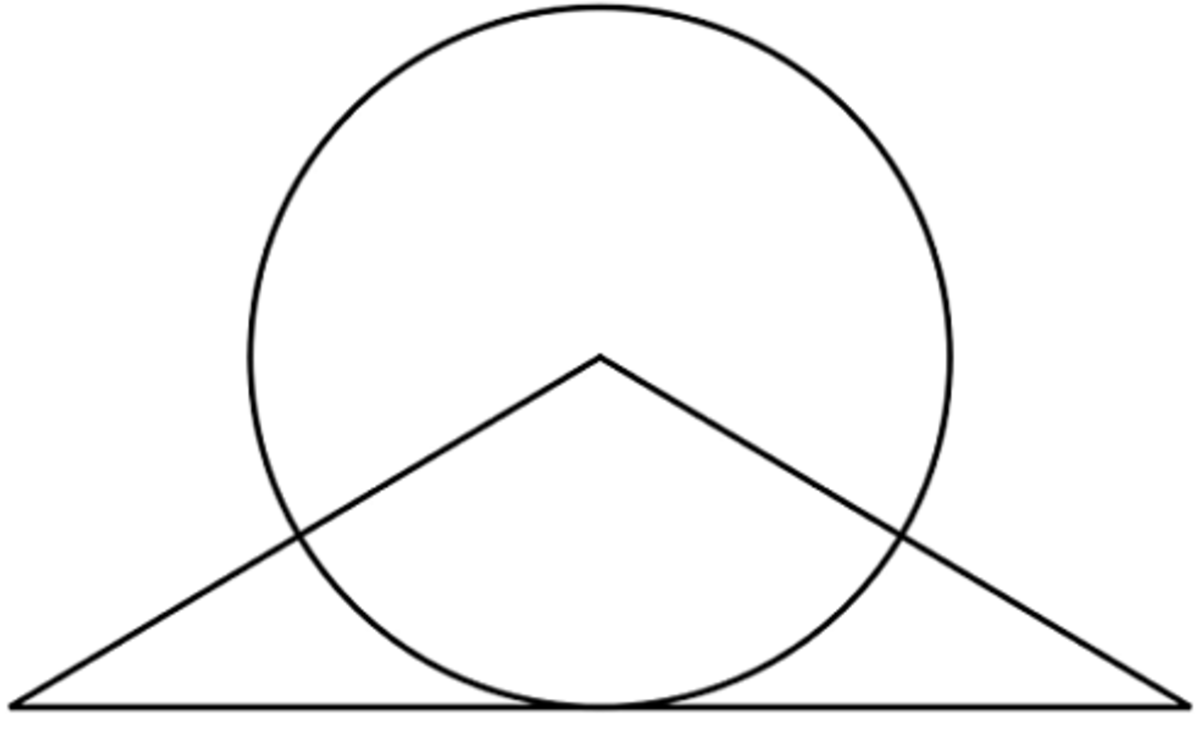
Relevant wiki: Circles Problem Solving - Basic

Short cut for MCQ:

If the unequal angle is 30 degrees, ratio of area of overlapping to non-overlapping is 30 360 = 1 12 \dfrac{30}{360} = \dfrac{1}{12} . There is no option of 1 12 \dfrac 1 {12} .

Therefore the equal angles are 30 degrees and non-equal angles is 120 degrees.

Therefore required ratio = 120 360 = 1 3 =\dfrac{120}{360}=\dfrac{1}{3} .

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...