There are 5 boxes and a cat
A cat hides in one of the 5 boxes labeled 1~5 from left to right, and you need to catch the cat.
Every night it switches places to an adjacent box; for example, if the cat was in #3 and didn't get caught during the day, it moves to #2 or to #4 in the night. Then, everyday when the night is over, you can check only 1 box to find the cat.
Applying the optimal strategy, you are guaranteed to find the cat in at most X days. What is X ?
Note: If the cat was in #5 during the day, it can only move to #4 in the night. Similarly, #1 has only one adjacent box, #2. The boxes are kept closed at all times, but the cat can slip through the folds on top during the night.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
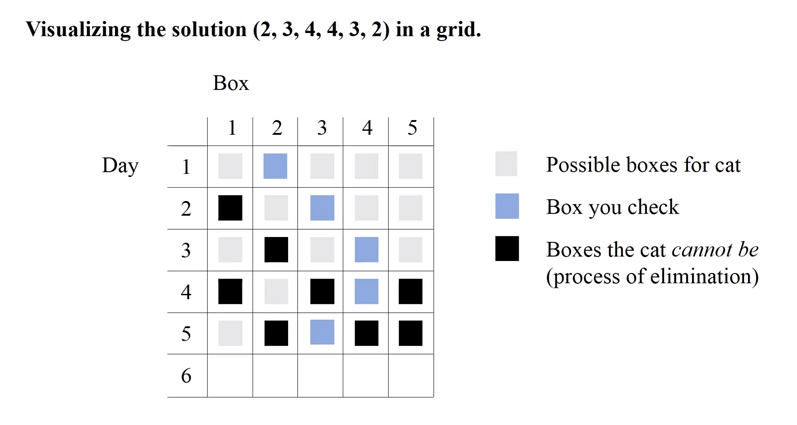
5 solutions
This is explained by preshtalwalker in youtube.
Log in to reply
Not only is it explained by preshtalwalker, the table is taken from his video as well without any credit.
This is damn hard
If you pay attention to the parity of the sum of days & boxes — (d + b) — your strategy can be summarized as follows: you ensure at each step that if the cat is in a box with a number smaller than the one you’re looking at, then (d + b) is even. If you still come up empty handed looking at the fourth box on the third day, then after that even parity for d + b becomes true for all the boxes, and you know that the cat will be in a box numbered less than or equal to four. Now you work back down — knowing that the cat can’t “slip by” you — eliminating the higher box-numbered, even d + b combinations as you go, finding the cat — if you haven’t already — in the second box on the sixth day. (The parity of d + b is even for the first box on the seventh day, but that state/position’s only predecessor is the second box on the sixth day, which you have already observed.)
Nice explanation and table. Post more problems like this!!! :)
The table makes the solution clearer than any words can. But, did you show that this solution is optimal? That is, could another strategy find the cat in 5 days? I think you'd have to show that at each day, looking in any other box leads to worse or equivalent results. For instance, on the 4th day, you could have looked in box 2.
You could have at least given Presh Talwalkar credit for the table from his video.
Let's find a formula for the total number of nights needed to find the cat if there are N boxes labelled b 1 , b 2 , . . . b N (because why not?). Let us label the nights n 1 , n 2 , . . . n X . To find the cat, we consider the worst case scenario (we will never find the cat until we are guaranteed to find the cat). Choosing a box near the middle does not help at first since the cat can jump into any box from the left or right. By the next night, the cat can still be in any box. The key is the edge of the row, where a cat can only jump in one direction. If the cat was in b 1 on a night n a after n 1 , then on the previous night n a − 1 , the cat must have been in b 2 . There is no other box adjacent to b 1 . Using the contrapositive: if we check b 2 and find the cat is not there, then the cat cannot be in b 1 the next night.
It is n 1 . Using the logic described above, we have to check b 2 . In all the following diagrams, if a box is white, the cat may be there. If it is black, it cannot be there. If it is red, the box has just been checked and the cat is not there.
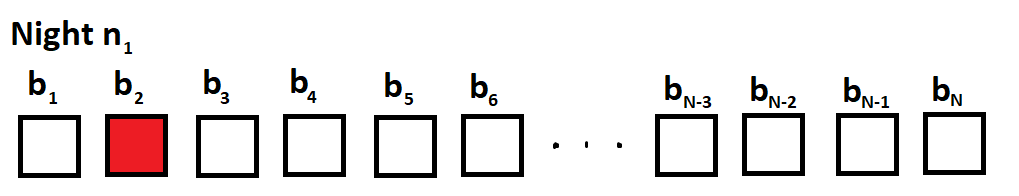
Now it is n 2 , and the cat is not in b 1 . If we check b 2 , then no progress will be made by the next night (we will have the same situation as tonight). Checking b 1 , which is redundant, or any box past b 3 is useless, as it does not eliminate the cat's possible boxes. However, if we check b 3 , and the cat is not there, we will find that the cat is not in a box adjacent to b 2 . Therefore, on n 3 , the cat will not be in b 2 .
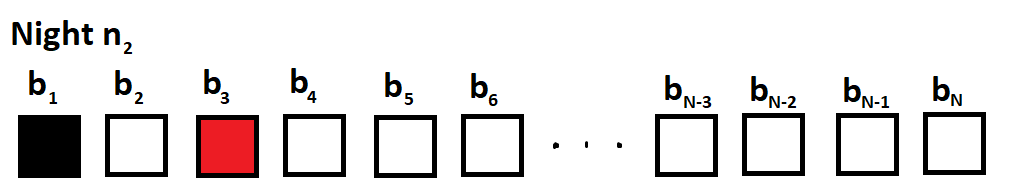
Now it is n 3 , and the cat is not in b 2 . Although the number of possible boxes is the same, this is the only decision that does not bring us back to a previous state. An important note is that b 1 is currently bordering the catless b 2 , so it will not have a cat on n 4 . Using similar logic as before, we find that checking any box beside b 4 brings us to a current or previous state on n 4 . Therefore, we check b 4 .
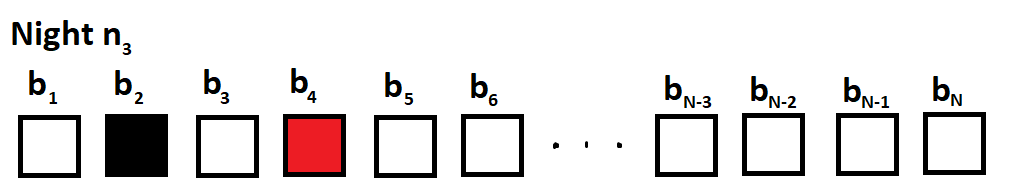
Now it is n 4 , and the cat is not in b 1 or b 3 . On n 5 , the cat cannot be in b 2 , since both b 1 and b 3 are catless. Note that on any night n a , the only box which we can check that puts the arrangement into a new state is b a + 1 . The pattern applies to tonight as well, so we will check b 5 .
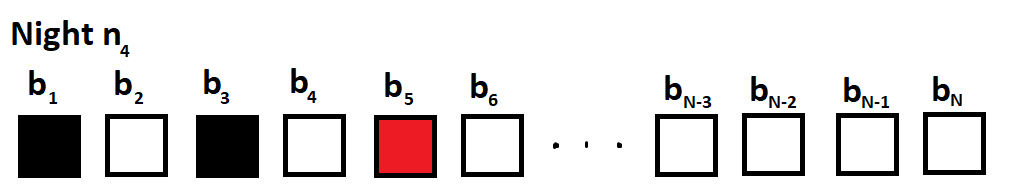
Now it is n 5 , and the cat is not in b 2 or b 4 . On n 6 , the cat will not be in b 1 or b 3 . If we check b 6 tonight, we will also eliminate b 5 .
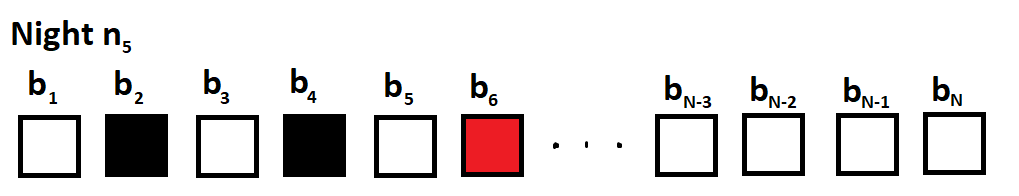
This process will continue. On night n a , we check b a + 1 . if a is odd, all even-numbered boxes before b a cannot have a cat, and if a is even, all odd-numbered boxes before b a cannot have a cat. Let us assume N is odd (for the sake of the diagram, but the same process will work if N is even). This is what n N − 2 looks like:

Now it is n N − 1 , and the cat cannot be in an odd-numbered box (including b N )! If we check an even-numbered box b a where 4 ≤ a ≤ N − 3 , the result is that on night n N , the cat cannot be in any even-numbered box. While this sounds promising, if the process is repeated, we would not make any progress (no additional boxes would ever be eliminated). Like before, the edge benefits us in that the cat only has one option. We will choose b 2 .

Now it is n N , and the cat is not in an even-numbered box or b 1 . Using similar logic as yesterday, tackling the edges is the best method, and observation quickly shows that b 3 is the box to choose.

On n N + 1 , box b 4 will be the box to choose. This process will continue, so for any night n a , we will check box b a − N + 3 . Here are a few more nights:
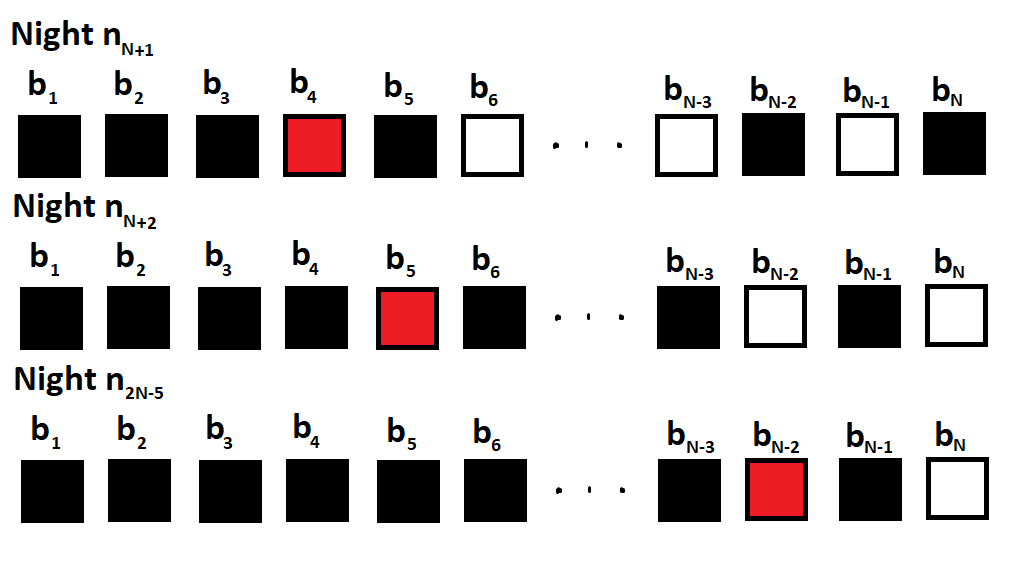
It is the final night, n 2 N − 4 . The cat must be in b N − 1 . We check the box and find the cat. The boxes we checked, in order, were: { b 2 , b 3 , b 4 , . . . b N − 2 , b N − 1 , b 2 , b 3 , b 4 , . . . b N − 2 , b N − 1 } . X = 2 N − 4 for N boxes. In this specific case, X = 2 ( 5 ) − 4 = 6 .
Excellent reasoning
Thank you for sharing, very clear explanation!
Your formula X=2N-4 doesn’t seem to work for N=1 or N=2.
Log in to reply
The reason is that there are no middle boxes in these examples.
Label boxes left to right 1,2,3,4,5. Checking box 2 twice eliminates any chance it started in box 1 originally. That leaves it now in box 3,4 or 5 after two checks. Now check box 4 twice. If not found it will have to have been in 3 at beginning of third check because 4 and 5 have now been eliminated as well. It would have moved twice while you checked box 4. It could have moved only two jumps, either from 3>2>1, or from 3>2>3. So check 3 (fifth check). If not there it must have been in 1 for check five and have no choice but to move to 2. Check 2. Last possible place it could be. Six checks total (Five really needed to know where exactly it is).
doesn't always work. take this case: cat starts in 4, you check 2. cat moves to 3, you check 2. cat moves to 2, you check 4. cat moves to 3, you check 4. cat moves to 4, you check 3. cat moves to 3 or 5, you check 2. you miss.
Checking 2 twice doesn't help because after the next jump it can still be at spots 2,3,4,5
Actually, you can conclude where he is only after 4 searches, at least indirectly.
i) Search in box 2, if not there next day he will be in either 2,3,4 or 5
ii) Search in box 3, if not there next day he will either be in 1,3,4 or 5.
iii) Search in box 4, if not there the next day he will either be in 2 or 4.
iv) Search in box 2, if not there you can conclude he is in box 4. QED.
If you want to find him directly, the next day he will either be in boxes 3 or 5.
v) Search in box 3, if not there you can conclude the next day he will be in box 4.
vi) Search in box 4, you found him!!!
best solution so far
Note that every night the cat changes from even to odd box or vice versa, so let us consider the case where the cat is in an even box i.e. the "even cat".
-
Open box 2. If not there it must have started in box 4.
-
Open box 3. If not there is can only have jumped to box 5.
-
Open box 4. If not there we can conclude that this was an "odd cat" to start with.
After 3 moves the cat is now an "even cat" so repeat the above.
Total box checks = 2 x 3 = 6
Lets consider only three boxes are there,
if at, Day 1- if the cat starts at 1st or 3rd box(odd numbered box) at the second day it must be in 2nd box OR If it starts at second box it will surely end up in either 1st or 3rd. And at this case we end up in the first situation were the cat starts in odd numbered box. so that the next day the cat should be in 2nd box.WE WIN!
So at three boxes situation we can find the cat in 2 days if we follow these steps---open(2 at day one,2 also in day two)
Now we can get to five boxes and solve it by the same odd or even method.
If started in even number,(2,4)
At Day 1, if the cat is in even number, at the next day it should surely end up in an odd numbered box(1,3,5). At Day 2, we know that it is in odd numbered box and lets open any odd numbered box At Day 3, so now it will eventually end up in a even numbered box. at day four we make sure that it should be in an odd box.
so to frame this as a solution we should pick(when we know that the cat is in) a box is, Day 1- 2nd box Day 2- 3rd box Day 3- 4th box It follows as (2,3,4),
If started in an odd number, we can follow the same procedure to find the cat,and also reverse of it, i.e (4,3,2) or (2,3,4).
so now we can combine the results so that giving a solution which will assure that we can find the cat by picking the boxes in order of(2,3,4,4,3,2) irrespective of luck which we can find the cat at the middle of this process.so the solution is in 6 days .
This process is posted in the image below (credit: presh talwalker's youtube channel "mind your decisions"), at the 6th day it should end up at the 2nd box only because we didn't find the cat in any of the trials