There is a way to do this in <60 seconds #1
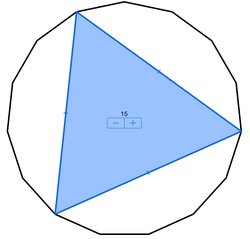 An equilateral triangle is formed by connecting every 5th vertex of a regular 15-gon (polygon with 15 sides). If the 15-gon has a side length of 1, find the area of the equilateral triangle. Give your answer to 2 decimal places.
An equilateral triangle is formed by connecting every 5th vertex of a regular 15-gon (polygon with 15 sides). If the 15-gon has a side length of 1, find the area of the equilateral triangle. Give your answer to 2 decimal places.
The answer is 7.51.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
@Niranjan Khanderia Thanks for the great solution! We converted your comment into a solution. If you subscribe to this thread, you will receive notifications about it.
Anti-solution: We notice that the 15-gon looks suspiciously like a bumpy circle, so we assume it actually is a circle. The circumference is 15, so the diameter is π 1 5 . We can solve for the side length of the triangle, which is 4 π 1 5 3 . Substituting into the formula A = 4 s 2 3 results in the answer of about 7.5.
Well ... that get you approximately close (so you get marked correct), but doesn't give you the correct value (so are you really correct?).
 ABCDEF are the five sides of the 15-gon, and AF one side of the equilateral triangle.
ABCDEF are the five sides of the 15-gon, and AF one side of the equilateral triangle.
The external angle between the sides of the 15-gon = 360/15 =24.
Because of symmetry, CD
∥
AF.
BC makes 24 angle with CD. So CD makes 24 angle with AF.
AB makes 24 angle with BC. So AB makes 24 + 24 = 48 angle with AF.
AF = projection of AB+BC+CD+DE+EF on AF
Because of symmetry, projections of AB & EF, and of BC & CD are equal.
AF=1 * Cos48 + 1 * Cos24 + 1 + 1 * Cos24 + 1 * Cos48.
R
e
q
u
i
r
e
d
A
R
E
A
o
f
e
q
u
i
l
a
t
e
r
a
l
△
=
4
3
∗
(
A
F
)
2
=
7
.
5
1
Hahah, anti-solution. Next time I post one like this I'll give it a longer side length so this technique doesn't work.
Solution 1 (quicker).
You may want to refer to this note
Basically, the area of any regular polygon created by joining every kth vertex of a regular n-sided polygon of side length a can be represented by the formula
8 k a 2 n ( cot n 1 8 0 k ) ( csc 2 ( n 1 8 0 ) ) ( 1 − cos ( n k 3 6 0 ) )
Solution 2:
assuming you don't know the formula (which you probably don't). We can find the radius by looking at the central angle
r = 2 csc ( 3 0 3 6 0 ) ≈ 2 . 4
Given the radius of an equilateral triangle, the area is A = 4 3 r 2 3
4 3 ( 2 . 4 ) 2 3 ≈ 7 . 5
(Using more than 2 digits of 2.4 will help make it more accurate of course)
We shall find the length of the triangle side from the 15-gon sides.
ABCDEF are the five sides of 15-gon so that AF is one side of the triangle.
The length of AF is the projection of ABCDEF on AF.
ABCDEFA is a six sided isosceles trapezoidal polygon.
So CD
∥
AF..
External angels between adjoining sides of 15-gon = 360/15=24
o
.
So BC makes 24
o
with CD and hence with AF.
AB makes 24
o
with BC and hence 24+24=48
o
with AF.
AF = projections of AB + BC + CD + DE + EF
= 1 * Cos48 + 1 * Cos24 +1 +1 * Cos24 + 1 * Cos48.
So, required area =
4
3
∗
(
1
∗
C
o
s
4
8
+
1
∗
C
o
s
2
4
+
1
+
1
∗
C
o
s
2
4
+
1
∗
C
o
s
4
8
)
2
=
7
.
5
1
totally wrong concept . according to me since the polygon has 15 sides .so we can divide the central angle by 15 . i.e 360/15=24. since the radius of the equilateral triangle is given by 2/3 (3)^1/2 2 side. since the centroid have the ratio 2:1.so using trigonometry we get 0.5/radius=sin(12), so radius is 2.5.therefore using 2/3 (3)^1/2*side=2.5 . from that we get side=4.33. therefore area= 8.11
A side of 15-gon subtends 24 ∘ at the center, forming an isosceles triangle whose angles are 24 ∘ , 78 ∘ and 78 ∘ . The radius of the "bumpy circle" r = cos 7 8 ∘ 0 . 5 = 2.4049 . Now, note that the equilateral triangle can be split into two and rearranged to form a rectangle of same area. The area of the rectangle turns out to be
A = l e n g t h × b r e a d t h = ( 2 3 . r ) × ( 2 3 ) . r = 4 3 3 . r 2 = 7 . 5 1 2 8 □
Simple and easy to understand this solution.
Another solution @Trevor Arashiro (Similar but much easier) (Involves a simpler and easier formula)
Radius of a regular polygon = ( 2 sin ( 1 8 0 / n ) s )
Now with the radius of the polygon, we can equate this with 3 2 of the median of the triangle ( Remember, its an equilateral triangle so everything coincides).
Now the length of the median will also be equal to the height of the triangle.
From the height we can deduce the side of the equilateral triangle and thus the area.
Wasn't this simple this way??
@Mehul Arora Check this out. :)
Yeah , i think this is an easier way...
Yes, it indeed is simple (looking)
I don't remember the problem though, So I can't find faults in this (if any)
I'll check out for errors later :)
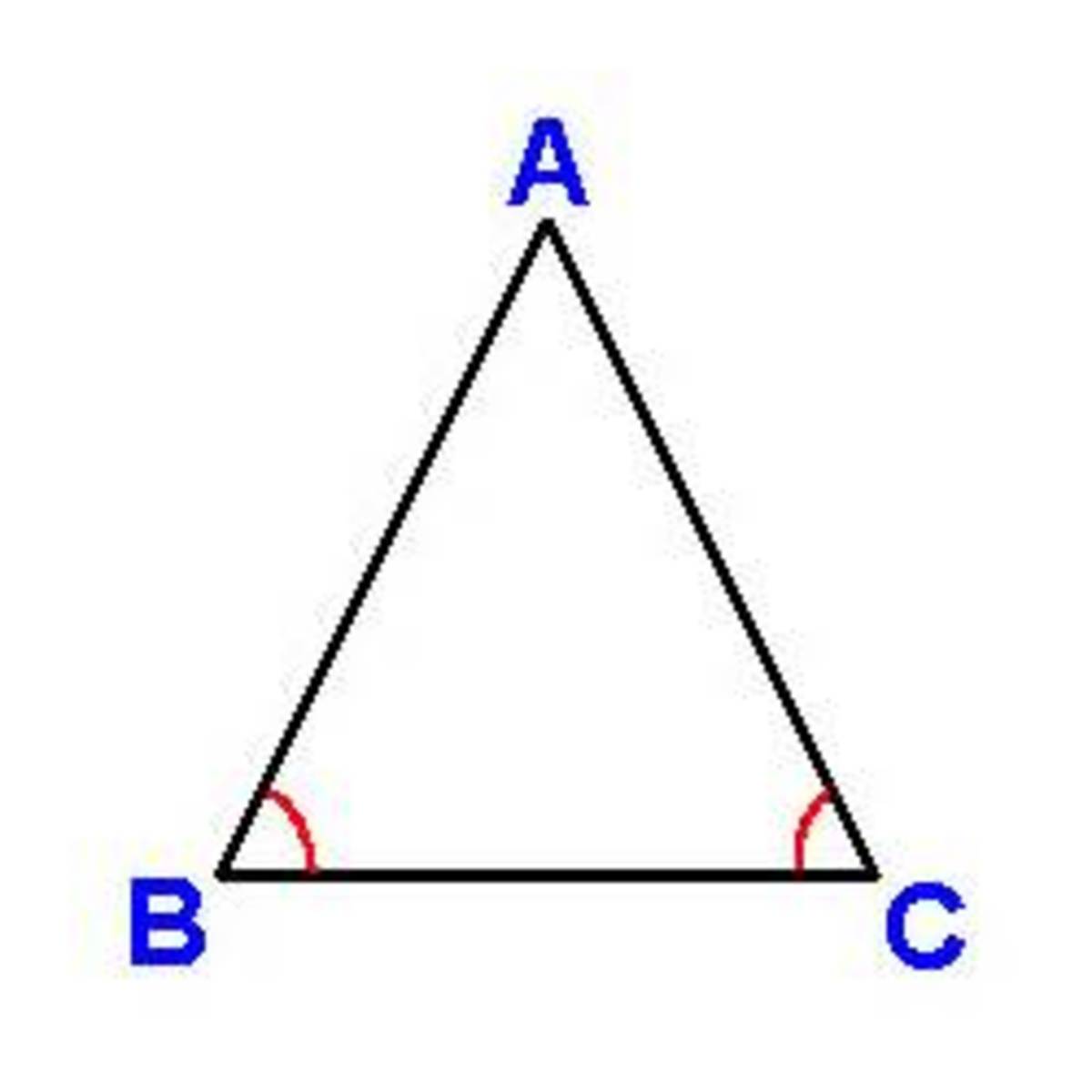
In △ A B C , ∠ B A C = 2 4 ∘ and A B = A C = r , a n d , B C = 1 .
Using the law of cosines ⟹
1 = 2 ∗ r 2 ∗ ( 1 − c o s ( 2 4 ∘ ) ) ⟹ r = 2 ∗ ( 1 − c o s ( 2 4 ∘ ) ) 1
Let x be the length of the given equilateral blue triangle, ⟹ 2 x = 2 3 ∗ r ⟹
x = 2 ∗ ( 1 − c o s ( 2 4 ∘ ) ) 3 ⟹ h e i g h t h = 2 3 ∗ 2 ∗ ( 1 − c o s ( 2 4 ∘ ) ) 3 ⟹
Area of the equilateral triangle A = 4 3 ∗ 2 ∗ ( 1 − c o s ( 2 4 ∘ ) ) 3 =
8 3 ∗ 3 ∗ ( 1 − c o s ( 2 4 ∘ ) 1 ) = 1 6 3 ∗ 3 ∗ ( s i n 2 ( 1 2 ∘ ) 1 ) = 7 . 5 1 to two decimal places.
Because there are so many side lengths, 15 to be exact. Simply inscribe the triangle within a circle that has a circumference of 15. Then, find the radius which is 15/2/pi. Draw a 120, 30, 30 triangle and drop a perpendicular line. Using that method, calculate the side length of the equilateral triangle. Then, plug in the side length for y in this equations. sqrt 3 X y sqrd divided by 4
First, make the assumption that a regular polygon is defined by at set of chords for a circle radius, R, where the chord defining angles are equal and sum to 360 degrees. Easily see that each angle is 360/n for a regular n-polygon (24 degree for n=15).
Using the equation for the length (a) of a chord : a = 2rSin( θ /2), we have two equations : one for the side of the 15-gon and 1 for the side of the inscribed triangle.
side of triangle = s = 2rSin(2 π /6)
side of 15-gon = 1 = 2r Sin(2 π /30)
Ratio our two equations ; we get:
triangle side, s = Sin( 6 2 π )/Sin( 3 0 2 π ) = 4.1654
using the equation for the area of an equilateral triangle, side s:
A = 4 3 s 2 = 7 . 5 1 3
In this solution there is no need to solve for the radius.
ABCDEF are the five sides of the 15-gon, and AF one side of the equilateral triangle. The external angle between the sides of the 15-gon = 360/15 =24. Because of symmetry, CD parallel to AF. BC makes 24 angle with CD. So CD makes 24 angle with AF. AB makes 24 angle with BC. So AB makes 24 + 24 = 48 angle with AF. AF = projection of AB+BC+CD+DE+EF on AF Because of symmetry, projections of AB & EF, and of BC & CD are equal. AF=1 * Cos48 + 1 * Cos24 + 1 + 1 * Cos24 + 1 * Cos48. So required area = sqroot3/4 * AF Which is equal to 7.51
The angle of the regular 15-gon = 156
the length of the side of the triangle = 2 sin 42 + 2 sin 66 + 1 = 4.16535
Area of triangle = 0.5 (4.16535)^2 sin 60 = 7.512838946
ABCDEF are the five sides of the 15-gon, and AF one side of the equilateral triangle.
The external angle between the sides of the 15-gon = 360/15 =24.
Because of symmetry, CD ∥ AF.
BC makes 24 angle with CD. So CD makes 24 angle with AF.
AB makes 24 angle with BC. So AB makes 24 + 24 = 48 angle with AF.
AF = projection of AB+BC+CD+DE+EF on AF
Because of symmetry, projections of AB & EF, and of BC & CD are equal.
AF=1 * Cos48 + 1 * Cos24 + 1 + 1 * Cos24 + 1 * Cos48.
R e q u i r e d A R E A o f e q u i l a t e r a l △ = 4 3 ∗ ( A F ) 2 = 7 . 5 1