Theres a faster construction

Construct two distinct arbitrary points on the line. Call them $A$ and $B$ . These require 0 moves. From each point, draw a circle which passes through $P$ , so a total of 2 moves. These circles intersect on $P$ and its reflection over the line $P'$ (By symmetry), so $PP'$ is perpendicular to $l$ . Constructing $PP'$ takes one move so there are a total of three moves.

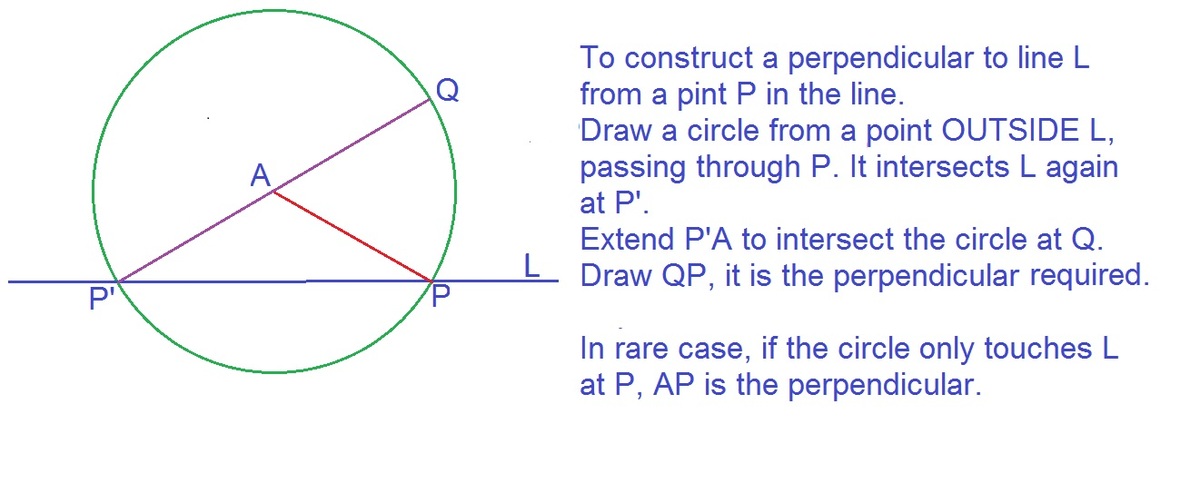
Just realised it said $P$ is on $l$ . In this case, construct an arbitrary point $A$ not on the $l$ . Let it be the centre of a circle passing through $P$ . If it intersects with $l$ only once, then it must be perpendicular, so it took only 2 moves. However, it is more likely to intersect $l$ again at $P'$ . Let the ray $AP'$ intersect the circle at $Q$ . By Thales' theorem, $\angle QPP'=90^{\circ}$ , so $QP$ is perpendicular to $l$ and it took 3 moves.