There's an applic- therom for that
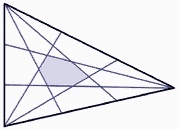Δ
A
B
C
has side lengths
4
,
5
1
and
5
3
. Each of its sides are trisected and lines are drawn to each point of trisection from their corresponding angle. By doing this, a hexagon is created in the middle of the triangle. The area of this hexagon can be represented by
p
=
x
(
x
−
1
)
(
x
−
2
)
2
+
x
where
x
is an integer and
p
is the area of the hexagon. Find
x
.
This problem is similar to one I posted previously but took down. This problem has different lengths and a different solution.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Are there any proofs for this theorem?
Log in to reply
There is, it uses a lot of coordinate geometry www.youtube.com/watch?v=XNaUDN65D1U
You can prove it using Routh's theorem, link is http://en.m.wikipedia.org/wiki/Routh's_theorem
This is such a silly way of asking a question... you can easily compute the area A by Heron's formula and given that x is an integer, the only 3 possible values for which the expression doesn't exceed A are 2, 3 and 4. You can't really get this wrong, even if you don't have a proof. There's too much additional information and the challenge in solving it is completely gone.
Let the points W , U , V , X , Y , Z be the points of trisection on A B , B C , C A respectively in that order. Note by Heron's formula, the area of the triangle is 9 0 . Now let B Z , C U meet at P, B Z , A Z meet at Q and A X , C U meet at R, and let the points D , E , F , G , H , I be the points of the hexagon that lie on the sides P Q , Q R , R P respectively in that order. Now the area of the hexagon equals
( P Q R ) − ( P D I ) − ( Q E F ) − ( R G H )
By Routh's theorem (http://en.m.wikipedia.org/wiki/Routh's_theorem), the corresponding areas are 7 9 0 , 7 9 , 7 9 , 7 9 so the area of the hexagon is 9 and then a little algebra reveals x = 3
Do u mean BZ, AX
And your solution surprised me. I thought Marion's was the only way.
Log in to reply
Not too surprising. Marion's theorem can be reduced to the equilateral triangle case (areas are changed by the same factor), which can then be proven using Routh's theorem.
This, in essence, is what @Daniel Remo did above.
But just a quick question, what would happen to Routh's when the triangle sides are broken into a ratio of 1:1:1. Then it's (1-1)^2*area. Which is 0 no matter what
Log in to reply
If you mean that we bisect each side (ie the the cevians are medians) then indeed the area is 0 which means they are concurrent. I.e you can use Routh's Theorem to show concurrency too :)
Marion Walter's Theorem states that such an hexagon formed by the side trisectors of any triangle has exactly 1 0 1 the area of the triangle. Using Heron's formula, triangle ABC is found to have an area of 9 0 . Hence, p = 9 . A little algebra gets you x = 3 .